题目内容
解不等式:
+
≤-1+x.
| kx |
| 5 |
| 1 |
| 2 |
考点:解一元一次不等式
专题:
分析:先去分母,再移项,合并同类项,再分2k-10>0与2k-10<0两种情况进行讨论.
解答:解:去分母得,2kx+5≤-10+10x,
移项得,2kx-10x≤-10-5,
合并同类项得,(2k-10)x≤-15,
当2k-10>0,即k>5时,x≤
,
当2k-10<0,即k<5时,x≥
.
移项得,2kx-10x≤-10-5,
合并同类项得,(2k-10)x≤-15,
当2k-10>0,即k>5时,x≤
| -15 |
| 2k-10 |
当2k-10<0,即k<5时,x≥
| -15 |
| 2k-10 |
点评:本题考查的是解一元一次不等式,熟知不等式的基本性质是解答此题的关键.

练习册系列答案
相关题目
已知关于x的一元二次方程x2-3x+2=0两实数根为x1、x2,则x1+x2=( )
| A、3 | B、-3 | C、1 | D、-1 |
关于x的一元二次方程x2-(2m-1)x+m+3=0的两根为x1,x2,且满足x1x2-x1-x2=1,则m的值为( )
| A、3 | ||
| B、-3 | ||
C、
| ||
D、-
|
已知|a|=5,|b|=8,且满足a<0,b<0,则a+b的值为( )
| A、3 | B、-3 | C、13 | D、-13 |
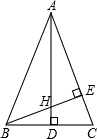 如图,△ABC中,AB=AC,AD⊥BC,BE⊥AC,AD和BE交于点H,且AE=BE,求证:AH=2BD.
如图,△ABC中,AB=AC,AD⊥BC,BE⊥AC,AD和BE交于点H,且AE=BE,求证:AH=2BD.