Question

【题目】在平面直角坐标系xOy中，A(t，0)，B，对于线段AB和x轴上方的点P给出如下定义：当∠APB＝60°时，称点P为AB的“等角点”．

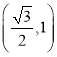(1)若，在点C(0，)，D，E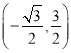中，线段AB的“等角点”是　 　；

(2)直线MN分别交x轴、y轴于点M、N，点M的坐标是(6，0)，∠OMN＝30°．

①线段AB的“等角点”P在直线MN上，且∠ABP＝90°，求点P的坐标；

②在①的条件下，过点B作BQ⊥PA，交MN于点Q，求∠AQB的度数；

③若线段AB的所有“等角点”都在△MON内部，则t的取值范围是　 　．

Answer 1

【答案】（1）C、D；（2）①，②∠AQB＝90°，③

【解析】

（1）根据给定的t值找出A、B点的坐标，再利用解三角形的方法讨论C、D、E点是否满足“等角点”的条件即可得出结论；

（2）①画出点N在y轴正半轴时图形，通过角的计算得出∠PAB＝∠OMN，从而得出“PA＝PM，AB＝BM”，再通过解直角三角形即可得出P点的坐标，同理可得出点N在y轴负半轴时的P点的坐标；②通过角的计算找出∠BMQ＝∠MQB＝30°，再结合外角的性质得出BQ＝BM＝AB即得出△ABQ是等边三角形，从而得出结论，同理点N在y轴负半轴时，结论相同；

（3）通过构建与y轴以及与线段MN相切的圆，找出点A与点B的临界点，求出此时的t值，从而得出线段AB的所有“等角点”都在△MON内部，则t的取值范围．

（1）当t＝﹣时，点A（﹣，0），点B（，0），

∵点C（0，），OC＝＝AB，且点O为线段AB的中点，

∴△ABC为等边三角形，

∴∠ACB＝60°，点C是线段AB的“等角点”；

∵点D（，1），B、D横坐标相等，

∴BD⊥x轴于点B．

∵AB＝﹣（﹣）＝，BD＝1﹣0＝1，tan∠ADB＝＝，

∴∠ADB＝60°，点D是线段AB的“等角点”；

∵点E（﹣，），A、E横坐标相等，

∴AE⊥x轴于点A．

∵AB＝﹣（﹣）＝，AE＝﹣0＝，tan∠AEB＝＝，

∴∠AEB≠60°，点E不是线段AB的“等角点”．

综上可知：点C、D是线段AB的“等角点”．

故答案为：C、D．

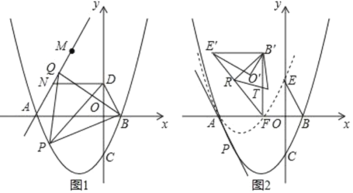
（2）①当点N在y轴正半轴时，如图1，

∵∠APB＝60°，∠ABP＝90°，

∴∠PAB＝30°，

又∵∠OMN＝30°，

∴PA＝PM，AB＝BM．

∵AB＝，

∴BM＝，

∴PB＝1．

∴P（6﹣，1）．

当点N在y轴负半轴时，同理可得点．

②当点N在y轴正半轴时，如图2，

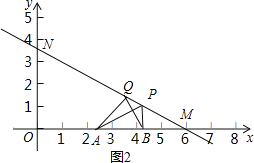
∵BQ⊥AP，且∠APB＝60°，

∴∠PBQ＝30°，

∴∠ABQ＝60°，

∴∠BMQ＝∠MQB＝30°，

∴BQ＝BM＝AB，

∴△ABQ是等边三角形．

∴∠AQB＝60°．

当点N在y轴负半轴时，同理可得∠AQB＝90°．

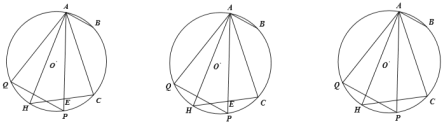
③以AB＝做底，AO′＝BO′为腰，∠AO′B＝120°作三角形，如图3所示．

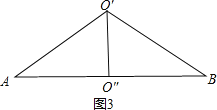
∵AO′＝BO′，AB＝，∠AO′B＝120°，

∴AO′＝1，O′O″＝．

（i）以直线y＝上的点O′为圆心，1为半径作圆，当圆O′与y轴相切，且O′在y轴右侧时，如图4所示，

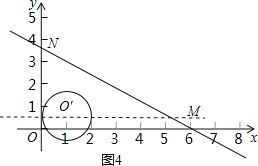
此时O′的坐标为（1，），此时A点的横坐标为1﹣AB＝1﹣，

即t＝1﹣；

（ii）以直线y＝上的点O′为圆心，1为半径作圆，当圆O′与线段MN相切，且O′在MN下方时，如图5所示．

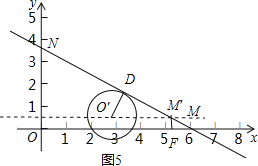
∵M′F＝，∠OMN＝30°，

∴MF＝＝．

∵O′D＝1，∠O′M′D＝∠OMN＝30°，

∴O′M′＝＝2．

此时点B的横坐标为OM﹣MF﹣O′M′+AB＝4，

∴t+＝4，t＝4﹣．

综上可知：若线段AB的所有“等角点”都在△MON内部，则t的取值范围是1﹣＜t＜4﹣．

故答案为：