题目内容
某商店经营一种小商品,进价为2.5元.据市场调查,销售单价是13.5元时平均每天销售量是500件,而销售价每降低1元,平均每天就可以多售出100件,每件小商品销售单价为多少元时,可以获利最多?(用两种方法解答)
考点:一元二次方程的应用
专题:销售问题
分析:根据等量关系“利润=(13.5-降价-进价)×(500+100×降价)”列出函数关系式.利用函数关系式求得利润最大值.
解答:解:设降价x元时利润最大为y元,
依题意:y=(13.5-x-2.5)(500+100x),
整理得:y=-100(x-3)2+6400(0≤x≤11);
∵a=-100<0,
∴当x=3时y取最大值,最大值是6400,
即降价3元时利润最大,
∴销售单价为10.5元时,最大利润6400元.
答:销售单价为10.5元时利润最大,最大利润为6400元.
依题意:y=(13.5-x-2.5)(500+100x),
整理得:y=-100(x-3)2+6400(0≤x≤11);
∵a=-100<0,
∴当x=3时y取最大值,最大值是6400,
即降价3元时利润最大,
∴销售单价为10.5元时,最大利润6400元.
答:销售单价为10.5元时利润最大,最大利润为6400元.
点评:此题考查二次函数的运用,运用了数学建模思想把实际问题转化为数学问题.运用函数性质求最值常用公式法或配方法.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
若x=-3是关于x的方程mx-2=0的解,则m的值是( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
下列运动属于平移的是( )
| A、荡秋千 |
| B、急刹车时,汽车在地面上的滑动 |
| C、风筝在空中随风飘动 |
| D、地球绕着太阳转 |
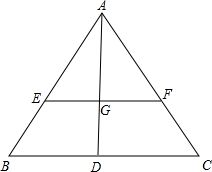 已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB、AC于点E、F.求AF:FC和EF:BC的值.
已知AD是△ABC的边BC上的中线,G是三角形的重心,EF过点G且平行于BC,分别交AB、AC于点E、F.求AF:FC和EF:BC的值.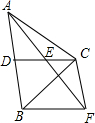 如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交于AE的延长线于F,连接BF.
如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交于AE的延长线于F,连接BF. 通过对苏科版九(上)教材一道习题的探索研究,“在一次聚会中,有45个人,每两个参加聚会的人都互相握了一次手,一共握了多少次手?”
通过对苏科版九(上)教材一道习题的探索研究,“在一次聚会中,有45个人,每两个参加聚会的人都互相握了一次手,一共握了多少次手?” 如图,△ABC=90°,∠1=∠B.如果AC=8,BC=6,AB=10,求CD的长.
如图,△ABC=90°,∠1=∠B.如果AC=8,BC=6,AB=10,求CD的长.