题目内容
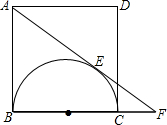 如图,以正方形ABCD边BC为直径,在正方形内作半圆O,过A作半圆的切线AF,切点为E,AF交BC的延长线于点F,求sin∠F的值.
如图,以正方形ABCD边BC为直径,在正方形内作半圆O,过A作半圆的切线AF,切点为E,AF交BC的延长线于点F,求sin∠F的值.考点:切线的性质,正方形的性质
专题:
分析:连接OE,根据切线的性质求得OE⊥AF,进而求得△ABF∽△OEF得出AF=2OF,设正方形的边长为1,再根据AF=2OF求出EF=
CF,设CF=x,则EF=2x,
即可表示出AF=1+2x,BC=1+x,AB=1,然后根据勾股定理求得CF,得出AF的值即可求出sin∠F;
| 1 |
| 2 |
即可表示出AF=1+2x,BC=1+x,AB=1,然后根据勾股定理求得CF,得出AF的值即可求出sin∠F;
解答: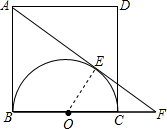 解:连接OE,
解:连接OE,
∵AF是半圆O的切线,
∴OE⊥AF,
∴∠B=∠OEF,∠AFB=∠OFE,
∴△ABF∽△OEF,
∴
=
=
,
∴AF=2OF,
设正方形的边长为1,
∴AB=BC=1,OC=
,
∵AB⊥CB,
∴AB是半圆O的切线,
∴AB=AE=1,
∴AE+EF=2(OC+CF),即1+EF=2(
+CF),
∴EF=
CF,
设CF=x,则EF=2x,
∴AF=1+2x,BC=1+x,AB=1,
∴根据勾股定理:12+(1+x)2=(1+2x)2,解得:x=
,
∴AF=1+2×
=
,
∴sin∠F=
=
=
.
 解:连接OE,
解:连接OE,∵AF是半圆O的切线,
∴OE⊥AF,
∴∠B=∠OEF,∠AFB=∠OFE,
∴△ABF∽△OEF,
∴
| AF |
| OF |
| AB |
| OE |
| 2 |
| 1 |
∴AF=2OF,
设正方形的边长为1,
∴AB=BC=1,OC=
| 1 |
| 2 |
∵AB⊥CB,
∴AB是半圆O的切线,
∴AB=AE=1,
∴AE+EF=2(OC+CF),即1+EF=2(
| 1 |
| 2 |
∴EF=
| 1 |
| 2 |
设CF=x,则EF=2x,
∴AF=1+2x,BC=1+x,AB=1,
∴根据勾股定理:12+(1+x)2=(1+2x)2,解得:x=
| 1 |
| 3 |
∴AF=1+2×
| 1 |
| 3 |
| 5 |
| 3 |
∴sin∠F=
| AB |
| AF |
| 1 | ||
|
| 3 |
| 5 |
点评:本题综合考查了相似三角形的判定与性质、勾股定理、正方形的性质以及锐角三角函数的定义等知识点.解题的关键在于根据已知条件找到相似三角形.

练习册系列答案
相关题目
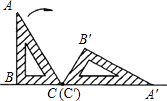 如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置.若AC=15cm,那么顶点A从开始到结束所经过的路径长为( )
如图,一块含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C′的位置.若AC=15cm,那么顶点A从开始到结束所经过的路径长为( )| A、10πcm | ||
B、10
| ||
| C、15πcm | ||
| D、20πcm |
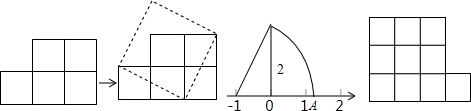
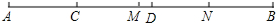 如图,已知C、D两点将线段AB分为三部分,且AC:CD:DB=2:3:4,若AB的中点为M,BD的中点为N,且MN=5cm,求AB的长.
如图,已知C、D两点将线段AB分为三部分,且AC:CD:DB=2:3:4,若AB的中点为M,BD的中点为N,且MN=5cm,求AB的长.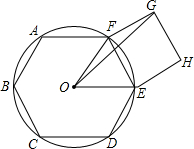 如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.
如图,半径为R的圆内,ABCDEF是正六边形,EFGH是正方形.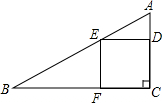 在Rt△ABC中,∠C=90°,AC=6,BC=12,在AC上有一动点D(不与A、C重合),作DE∥BC交AB于点E,作EF∥AC交BC于点F.当点D在什么位置时,四边形CDEF的面积最大?
在Rt△ABC中,∠C=90°,AC=6,BC=12,在AC上有一动点D(不与A、C重合),作DE∥BC交AB于点E,作EF∥AC交BC于点F.当点D在什么位置时,四边形CDEF的面积最大?