题目内容
 如图所示,在△ABC中,E为中线AD上一点,
如图所示,在△ABC中,E为中线AD上一点,| DE |
| AE |
| 1 |
| 2 |
考点:三角形的重心
专题:证明题
分析:取AC中点F′,连结DF′,BF′,BF′交AD于E′.根据三角形中位线定理可得DF′∥AB,DF′=
AB,再由△DE′F′∽△AE′B,证明E′与E重合,进而根据两点确定一条直线可得F′与F重合.
| 1 |
| 2 |
解答: 证明:取AC中点F′,连结DF′,BF′,BF′交AD于E′.
证明:取AC中点F′,连结DF′,BF′,BF′交AD于E′.
∵D为BC中点,F′为AC中点,
∴DF′∥AB,DF′=
AB,
∴△DE′F′∽△AE′B,
∴
=
=
,
∵
=
,
∴
=
=
,
∴
=
=
,
∵E、E′都是中线AD上的点,
∴E′与E重合,
∵两点确定一条直线
∴BE与AC的交点F′与F重合,
∴AF=CF.
 证明:取AC中点F′,连结DF′,BF′,BF′交AD于E′.
证明:取AC中点F′,连结DF′,BF′,BF′交AD于E′.∵D为BC中点,F′为AC中点,
∴DF′∥AB,DF′=
| 1 |
| 2 |
∴△DE′F′∽△AE′B,
∴
| DE′ |
| AE′ |
| DF′ |
| AB |
| 1 |
| 2 |
∵
| DE |
| AE |
| 1 |
| 2 |
∴
| DE′ |
| AE′ |
| DE |
| AE |
| 1 |
| 2 |
∴
| DE′ |
| DA |
| DE |
| DA |
| 1 |
| 3 |
∵E、E′都是中线AD上的点,
∴E′与E重合,
∵两点确定一条直线
∴BE与AC的交点F′与F重合,
∴AF=CF.
点评:本题实际上考查了三角形的重心的性质,三角形的重心是三角形三边中线的交点,重心到顶点的距离与重心到对边中点的距离之比为2:1.准确作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列四个函数中,当x>0时,y随x的增大而减小的是( )
| A、y=3x | ||
| B、y=x-1 | ||
C、y=-
| ||
D、y=
|
人的正常体温约是37℃,我们把体温超过正常体温的部分记作正数,那么-0.2℃表示( )
| A、体温为零下0.2℃ |
| B、体温为零上0.2℃ |
| C、体温为37.2℃ |
| D、体温为36.8℃ |
下列方程中,关于x的一元二次方程是( )
A、
| ||||
| B、3(x+1)2=2(x+1) | ||||
C、
| ||||
| D、2x2-3xy+y2=9 |

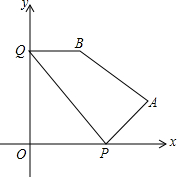 如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.
如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.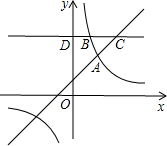 如图,一次函数y=kx+1(k≠0)与反比例函数y=
如图,一次函数y=kx+1(k≠0)与反比例函数y=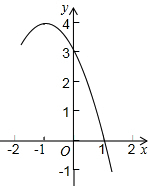 已知抛物线y=-x2+bx-c的部分图象如图所示.
已知抛物线y=-x2+bx-c的部分图象如图所示.