题目内容
【题目】观察下列各式及其展开式
（a+b）2＝a2+2ab+b2
（a+b）3＝a3+3a2b+3ab2+b3
（a+b）4＝a4+4a3b+6a2b2+4ab3+b4
…
根据下图，猜想：
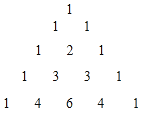
（a+b）5＝_____．
【答案】a5+5a4b+10a3b2+10a2b3+5ab4+b5．
【解析】
根据题意得出展开项的系数规律，分别表示出（a+b）5的展开式．
解：（a+b）2＝a2+2ab+b2，
（a+b）3＝a3+3a2b+3ab2+b3，
（a+b）4＝a4+4a3b+6a2b2+4ab3+b4，
（a+b）5＝a5+5a4b+10a3b2+10a2b3+5ab4+b5，
故答案为：a5+5a4b+10a3b2+10a2b3+5ab4+b5．
练习册系列答案
相关题目
【题目】在一个不透明的口袋里装有颜色不同的红、白两种颜色的球共5只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 38 | 51 | 76 | 195 | 324 | 401 |
摸到白球的频率 | 0.38 | 0.34 | 0.38 | 0.39 | 0.405 | 0.401 |
（1）请估计：当n很大时，摸到白球的频率将会接近_______；（精确到0.1）
（2）试估算口袋中白球有多少只？
（3）请画树状图或列表计算：从中先摸出一球，不放回，再摸出一球；摸到两只白球的概率是多少？
