Question

【题目】如图，正方形ABCD内接于⊙O，E为弧CD上任意一点，连接DE，AE.

(1)求∠AED的度数；

(2)如图②，过点B作BF∥DE交⊙O于点F，连接AF，AF＝1，AE＝4，求DE的长度．

Answer 1

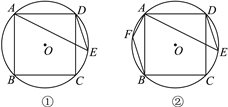
【答案】（1）∠AED＝45°；（2）或

【解析】

（1）图1中，连接OA、OD．根据∠AED＝∠AOD，只要证明∠AOD＝90°即可解决问题；

（2）图2中，连接CF、CE、CA，作DH⊥AE于H．首先证明CE＝AF＝1，求出AC、AD，设DH＝EH＝x，在Rt△ADH中，利用勾股定理即可解决问题.

（1）如图①，连接OA，OD.

∵四边形ABCD是正方形，

∴∠AOD＝90°，

∴∠AED＝∠AOD＝45°.

(2)如图②，连接CF，CE，CA，作DH⊥AE于点H，

∵BF∥DE，AB∥CD，

∴∠ABF＝∠CDE.

∵∠CFA＝∠AEC＝90°，

∴∠DEC＝∠AFB＝135°.

∵CD＝AB，

∴△CDE≌△ABF，

∴AF＝CE＝1，

∴AC＝，

∴AD＝AC＝，

∵∠DHE＝90°，

∴∠HDE＝∠HED＝45°，

∴DH＝HE，设DH＝HE＝x.

在Rt△ADH中，

∵AD2＝AH2＋DH2，

∴＝(4－x)2＋x2，

解得x＝或，

∴DE＝DH＝或.