题目内容
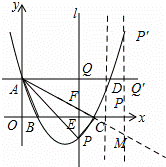
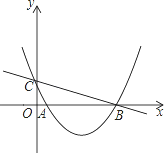
如图,在平面直角坐标系中,抛物线y=mx2﹣8mx+4m+2(m>2)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2﹣x1=4,直线AD∥x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q.
(1)求抛物线的解析式;
(2)当0<t≤8时,求△AP C面积的最大值;
C面积的最大值;
(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与△AOB相似?若存在,求出此时t的值; 若不存在,请说明理由.
若不存在,请说明理由.
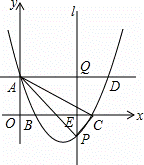
解:(1)由题意知x1、x2是方程mx2﹣8mx+4m+2=0的两根,
∴x1+x2=8,
由
解得: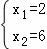
∴B(2,0)、C(6,0)
则4m﹣16m+4m+2=0,
解得:m=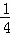 ,
,
∴该抛物线解析式为:y= ;
;
(2)可求得A(0,3)
设直线AC的解析式为:y=kx+b,
∵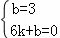
∴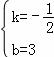
∴直线AC的解析式为:y=﹣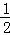 x+3,
x+3,
要构成△APC,显然t≠6,分两种情况讨论:
①当0<t<6时,设直线l与AC交点为F,则:F(t,﹣ ),
),
∵P(t, ),∴PF=
),∴PF=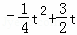 ,
,
∴S△APC=S△APF+S△CPF
=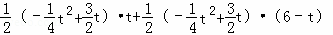
=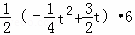
=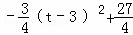 ,
,
此时最大值为: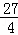 ,
,
②当6≤t≤8时,设直线l与AC交点为M,则:M(t,﹣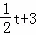 ),
),
∵P(t, ),∴PM=
),∴PM= ,
,
∴S△APC=S△APF﹣S△CPF=
=
= ,
,
当t=8时,取最大值,最大值为:12,
综上可知,当0<t≤8时,△APC面积的最大值为12;
(3)如图,连接AB,则△AOB中,∠AOB=90°,AO=3,BO=2,
Q(t,3),P(t,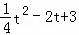 ),
),
①当2<t≤6时,AQ=t,PQ=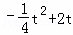 ,
,
若:△AOB∽△AQP,则: ,
,
即: ,
,
∴t=0(舍),或t=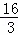 ,
,
若△AOB∽△PQA,则: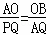 ,
,
即: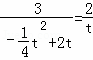 ,
,
∴t=0(舍)或t=2(舍),
②当t>6时,AQ′=t,PQ′=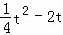 ,
,
若:△AOB∽△AQP,则: ,
,
即: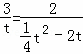 ,
,
∴t=0(舍),或t=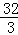 ,
,
若△AOB∽△PQA,则: ,
,
即: ,
,
∴t=0(舍)或t=14,
∴t= 或t=
或t= 或t=14.
或t=14.

下列四个命题中,真命题是( )
|
| A. | “任意四边形内角和为360°”是不可能事件 |
|
| B. | “湘潭市明天会下雨”是必然事件 |
|
| C. | “预计本题的正确率是95%”表示100位考生中一定有95人做对 |
|
| D. | 抛掷一枚质地均匀的硬币,正面朝上的概率是 |
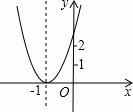
已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
|
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )

|
| A. | 110° | B. | 80° | C. | 70° | D. | 60° |

 (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.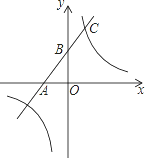
 ﹣
﹣ ;③|﹣2|=2.
;③|﹣2|=2.