题目内容
4.已知关于x的方程$\frac{1-x}{x-2}+2=\frac{k}{2-x}$有解,则k的取值范围是k≠1.分析 首先去分母可得x=3-k,根据分式方程有解则x-2≠0,进而可得x≠2,则3-k≠2,再解即可.
解答 解:去分母得:1-x+2(x-2)=-k,
1-x+2x-4=-k,
x-3=-k,
x=3-k,
∵关于x的方程$\frac{1-x}{x-2}+2=\frac{k}{2-x}$有解,
∴x-2≠0,
x≠2,
∴3-k≠2,
解得:k≠1,
故答案为:k≠1.
点评 此题主要考查了分式方程的解,关键是掌握分式方程有解时,分母不为零可得x的取值范围,进而可得k的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列计算正确的是( )
| A. | -22=-4 | B. | -1-3=-2 | C. | (-3)2=6 | D. | (-1)3=1 |
13. 如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
 如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )
如图,四边形ABCD内接于半圆O,已知∠ADC=140°,则∠AOC的大小是( )| A. | 40° | B. | 60° | C. | 70° | D. | 80° |
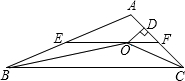 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①∠BOC=90°+$\frac{1}{2}∠A$;②EF=BE+CF;③设OD=m,AE:AF=n,则S△AEF=$\frac{1}{2}mn$;④EF是△ABC的中位线.其中正确的结论是 ( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①∠BOC=90°+$\frac{1}{2}∠A$;②EF=BE+CF;③设OD=m,AE:AF=n,则S△AEF=$\frac{1}{2}mn$;④EF是△ABC的中位线.其中正确的结论是 ( )