题目内容
 26、如图,已知点P在∠AOB的边OA上,
26、如图,已知点P在∠AOB的边OA上,(1)按下列要求作图:
①作∠AOB的平分线OM;
②以P为顶点,作∠APQ=∠AOB,PQ交OM于点C;
③过C作CD⊥OB,垂足为点D.
(2)当PC=2CD时,求∠AOB的大小.
分析:(1)①以点O为圆心,以任意长为半径画弧与∠AOB的两边分别相交,再以两交点为圆心,以大于两交点之间的距离的一半为半径画弧,相交于一点,过这一点与O作射线OM即可;
②根据作一个角等于已知角的做法作出即可;
③以点C为圆心,以大于点C到OB的距离为半径画弧,与AB相交于两点,再分别以这两点为圆心,以大于两点之间的距离的一半为半径画弧,两弧相交于一点,过这一点与点C作直线,与OB相交于点D,则CD就是所要作的线段.
(2)过点C作CH⊥OA于点H,根据角平分线上的点到角的两边的距离相等可得CH=CD,再利用30°所对的直角边等于斜边的一半进行解答.
②根据作一个角等于已知角的做法作出即可;
③以点C为圆心,以大于点C到OB的距离为半径画弧,与AB相交于两点,再分别以这两点为圆心,以大于两点之间的距离的一半为半径画弧,两弧相交于一点,过这一点与点C作直线,与OB相交于点D,则CD就是所要作的线段.
(2)过点C作CH⊥OA于点H,根据角平分线上的点到角的两边的距离相等可得CH=CD,再利用30°所对的直角边等于斜边的一半进行解答.
解答: 解:(1)如图1所示,即为所要求作的图形.
解:(1)如图1所示,即为所要求作的图形.
按步骤完成作图过程(3分);
(2)如图2,过点C作CH⊥OA,垂足为H,(1分)
∵OM平分∠AOB,CD⊥OB,
∴CH=CD,
∵PC=2CD,
∴PC=2CH,
∴在△PCH中,∠HPC=30°,(1分)
∴∠AOB=30°.(1分)
 解:(1)如图1所示,即为所要求作的图形.
解:(1)如图1所示,即为所要求作的图形.按步骤完成作图过程(3分);
(2)如图2,过点C作CH⊥OA,垂足为H,(1分)
∵OM平分∠AOB,CD⊥OB,
∴CH=CD,
∵PC=2CD,

∴PC=2CH,
∴在△PCH中,∠HPC=30°,(1分)
∴∠AOB=30°.(1分)
点评:本题主要考查了角平分线的作法,作一个角等于已知角,过直线外一点作已知直线的垂线,都是基本作图,需要熟练掌握,另外还考查了角平分线上的点到角的两边的距离相等的性质,30°角所对的直角边等于斜边的一半的性质.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目

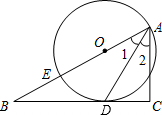 如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证:
如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相切于点D,∠B=30°.求证: 如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC.
如图,已知点O在∠BAC的平分线上,BO⊥AC,CO⊥AB,垂足分别为D、E,求证:OB=OC. 如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=
如图,已知点C在以AB为直径的⊙O上,点D在AB的延长线上,∠BCD=∠A,过点C作CE⊥AB于E,CE=8,cosD=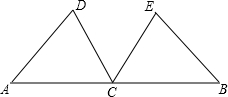 如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.
如图:已知点C在线段AB的中点,点D、E在线段AB的同侧,AD∥CE,AD=CE.