题目内容
证明式子20092+20092×20102+20102的结果为平方数．
考点：因式分解的应用
专题：
分析：根据所给代数式的结构特点，设a=2009，将所给的代数式恒等变形，运用因式分解法将代数式化为完全平方式的形式．
解答：解：设a=2009，则原式=a2+a2（a+1）2+（a+1）2=a2（a2+2a+2）+a2+2a+1
=a4+2a3+2a2+a2+2a+1
=（a4+2a2+1）+（2a3+2a）+a2
=（a2+1）2+2a（a2+1）+a2
=（a2+1+a）2
=（20092+2009+1）2，
故20092+20092×20102+20102的结果为平方数
=a4+2a3+2a2+a2+2a+1
=（a4+2a2+1）+（2a3+2a）+a2
=（a2+1）2+2a（a2+1）+a2
=（a2+1+a）2
=（20092+2009+1）2，
故20092+20092×20102+20102的结果为平方数
点评：该命题考查了因式分解及其应用问题；由于所给代数式中的数字较大，运用换元法可简化运算、容易发现代数式中数字之间的结构关系；灵活运用换元法是解题的关键．
练习册系列答案
相关题目
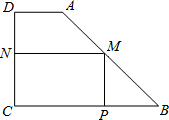如图所示，有一块形状是直角梯形的铁皮ABCD，它的上底AD=15cm，下底BC=40cm，垂直于底的腰CD=30cm，现要截成一块矩形铁皮MPCN，使它的顶点M、P、N分别在AB、BC、CD边上，求矩形MPCN的面积S关于MN的长x的函数关系式．
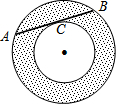如图，两个同心圆⊙O，大圆弦AB切小圆于一点C，AB=8，则图中圆环（即阴影部分）的面积
如图，点C、E、B、F在同一直线上，AB∥DE，A C∥DF，AC=DF，判断CE与FB的数量关系，证明你的结论．
如图所示，AB=AD，AC=AE，∠1=∠2，BC=12cm；求DE的长．