题目内容
17、若|a-2|+b2-2b+1=0，则a=
2
，b=1
．分析：本题应对方程进行变形，将b2-2b+1化为平方数，再根据非负数的性质“两个非负数相加，和为0，这两个非负数的值都为0”来解题．
解答：解：原方程变形为：|a-2|+（b-1）2=0，
∴a-2=0或b-1=0，
∴a=2，b=1．
∴a-2=0或b-1=0，
∴a=2，b=1．
点评：本题考查了非负数的性质，两个非负数相加，和为0，这两个非负数的值都为0．
练习册系列答案
相关题目
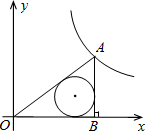（2012•桐乡市三模）如图，点A（a，b）在双曲线