题目内容
3.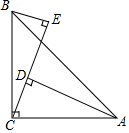 如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E,D,AD=25,DE=17,则BE=8.
如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E,D,AD=25,DE=17,则BE=8.
分析 可先证明△BCE≌△CAD,可求得CE=AD,结合条件可求得CD,则可求得BE.
解答 解:∵∠ACB=90°,
∴∠BCE+∠ACD=90°,
又∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=90°,
∴∠BCE+∠CBE=90°,
∴∠CBE=∠ACD,
在△CBE和△ACD中,$\left\{\begin{array}{l}{∠E=∠ADC}&{\;}\\{∠CBE=∠ACD}&{\;}\\{BC=AC}&{\;}\end{array}\right.$,
∴△CBE≌△ACD(AAS),
∴BE=CD,CE=AD=25,
∵DE=17,
∴CD=CE-DE=AD-DE=25-17=8,
∴BE=CD=8;
故答案为:8.
点评 本题主要考查全等三角形的判定和性质;证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11. 如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )
如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )
 如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )
如图,AB=AC,AE=EC,∠ACE=28°,则∠B的度数是( )| A. | 60° | B. | 70° | C. | 76° | D. | 45° |
18.一种面粉的质量标识为“25±0.25千克”,则下列面粉中合格的有( )
| A. | 24.70千克 | B. | 25.32千克 | C. | 25.51千克 | D. | 24.86千克 |
8.在△ABC中,AB=3cm,AC=5cm.若BC的长为整数,则BC的长可能是( )
| A. | 7cm | B. | 8cm | C. | 1cm | D. | 2cm |
15.已知a-2b=5,则2a-4b+$\frac{5}{2b-a}$的值( )
| A. | 9 | B. | -3 | C. | -15 | D. | 5 |
 如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.
如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.