题目内容
4.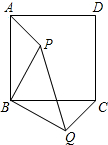 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBQ重合,若PB=3,求PQ的长为3$\sqrt{2}$.
如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBQ重合,若PB=3,求PQ的长为3$\sqrt{2}$.
分析 根据正方形的性质得到BA=BC,∠ABC=90°,再利用旋转的性质得到BP=BQ,∠PBQ=∠ABC=90°,于是可判断△PBQ为等腰直角三角形,然后根据等腰直角三角形的性质求解.
解答 解:∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∵△ABP绕点B顺时针方向旋转能与△CBQ重合,
∴BP=BQ,∠PBQ=∠ABC=90°,
∴△PBQ为等腰直角三角形,
∴PQ=$\sqrt{2}$PB=3$\sqrt{2}$.
故答案为3$\sqrt{2}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 在平行四边形ABCD中,已知AD=10cm,AB垂直于BD,点O是两条对角线的交点,OD=4cm,则AB=6cm.
在平行四边形ABCD中,已知AD=10cm,AB垂直于BD,点O是两条对角线的交点,OD=4cm,则AB=6cm.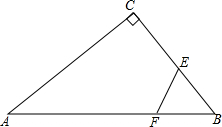 如图,Rt△ABC中,∠ACB=90°,AB=8cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<4).
如图,Rt△ABC中,∠ACB=90°,AB=8cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<4). 如图,在△ABC中,AB>AC,AD为∠BAC的平分线,AD的垂直平分线交BC的延长线于点F,交AB、AC于点E、G.
如图,在△ABC中,AB>AC,AD为∠BAC的平分线,AD的垂直平分线交BC的延长线于点F,交AB、AC于点E、G.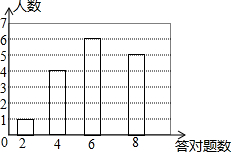 计算机网络知识竞赛,答对1题得10分,某次竞赛结果如图所示(每位参赛选手至少答对2题)
计算机网络知识竞赛,答对1题得10分,某次竞赛结果如图所示(每位参赛选手至少答对2题)