题目内容
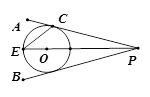
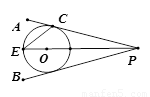
如图,点O在∠APB的平分在线,圆O与PA相切于 点C;
(1) 求证:直线PB与圆O相切;
(2) PO的延长线与圆O交于点E。若圆O的半径为3,PC=4。求弦CE的长。
 |
(1) 证明:过点O作OD⊥PB于点D,连接OC。∵PA切圆O于点C,
∴OC⊥PA。又∵点O在∠APB的平分线上,
∴OC=OD。∴PB与圆O相切。
(2) 解:过点C作CF⊥OP于点F。在Rt△PCO中,PC=4,OC=3,
OP=5,![]() =5,∵OC?PC=OP?CF=2S△PCO,
=5,∵OC?PC=OP?CF=2S△PCO,
∴CF=![]() 。在Rt△COF中,OF=
。在Rt△COF中,OF=![]() =
=![]() 。∴EF=EO+OF=
。∴EF=EO+OF=![]() ,
,
∴CE=![]() =
=![]() 。
。
 |

练习册系列答案
相关题目
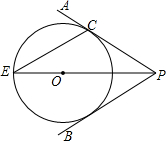 如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
如图,点O在∠APB的平分线上,⊙O与PA相切于点C.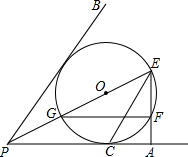 (2012•湖北模拟)如图,点O在∠APB的平分线上,⊙O与PA边相切于点C,
(2012•湖北模拟)如图,点O在∠APB的平分线上,⊙O与PA边相切于点C,