题目内容
如图，直线AC：y=
| ||
| 3 |
4
| ||
| 3 |
（1）求C点坐标；
（2）动点P从A出发，以2个单位每秒的速度沿AC运动到C点，运动时间为t秒（t＞0），设PM的长为d，求d与t的函数解析式，直接写出自变量的取值范围；
（3）在（2）的条件下，是否存在t值，使△PCB为等腰三角形？若存在，请求出t值；若不存在，请说明理由．
考点：一次函数综合题,等腰三角形的性质
专题：
分析：（1）由y轴垂直平分BC于D，AB=BC=4，得出C点的横坐标为2，代入解析式即可求得；
（2）先求出点A，点M，点C的坐标，求出AM，CM，①当0＜t≤
时，d=
-2t，②当
＜t≤2
时，d=2t-
，
（3）△PCB为等腰三角形，分类讨论：①当PC=BC时；②当PB=PC时；③PB=BC（不符合题意，舍去）；逐个求解．
（2）先求出点A，点M，点C的坐标，求出AM，CM，①当0＜t≤
4
| ||
| 3 |
8
| ||
| 3 |
4
| ||
| 3 |
| 3 |
8
| ||
| 3 |
（3）△PCB为等腰三角形，分类讨论：①当PC=BC时；②当PB=PC时；③PB=BC（不符合题意，舍去）；逐个求解．
解答：解（1）∵y轴垂直平分BC于D，AB=BC=4，
∴C点的横坐标为2，
∴y=
×2+
=2
，
∴点C的坐标为（2，2
），
（2）∵直线AC：y=
x+
与y轴交于点M，与x轴交于点A，
∴A点的坐标为（-4，0），M点的坐标为（0，
），
∴AM=
=
，
∵点C的坐标为（2，2
），
∴CM=
=
，
①当0＜t≤
时，
d=
-2t，
②当
＜t≤2
时，
d=2t-
，
（3）①∵BC=4，
∴当PC=4时，△PCB为等腰三角形，
d=AC-CP=4
-4，
代入d=
-2t，
得4
-4=
-2t．
解得t=2-
，
∴当t=2-
时，△PCB为等腰三角形，
②∵y轴垂直平分BC于D，
∴当P点到达M点时，△PCB为等腰三角形，
即t=
÷2=
，
∴使△PCB为等腰三角形的t的值为：2-
或
．
∴C点的横坐标为2，
∴y=
| ||
| 3 |
4
| ||
| 3 |
| 3 |
∴点C的坐标为（2，2
| 3 |
（2）∵直线AC：y=
| ||
| 3 |
4
| ||
| 3 |
∴A点的坐标为（-4，0），M点的坐标为（0，
4
| ||
| 3 |
∴AM=
42+(
|
8
| ||
| 3 |
∵点C的坐标为（2，2
| 3 |
∴CM=
(2
|
4
| ||
| 3 |
①当0＜t≤
4
| ||
| 3 |
d=
8
| ||
| 3 |
②当
4
| ||
| 3 |
| 3 |
d=2t-
8
| ||
| 3 |
（3）①∵BC=4，
∴当PC=4时，△PCB为等腰三角形，
d=AC-CP=4
| 3 |
代入d=
8
| ||
| 3 |
得4
| 3 |
8
| ||
| 3 |
解得t=2-
2
| ||
| 3 |
∴当t=2-
2
| ||
| 3 |
②∵y轴垂直平分BC于D，
∴当P点到达M点时，△PCB为等腰三角形，
即t=
8
| ||
| 3 |
4
| ||
| 3 |
∴使△PCB为等腰三角形的t的值为：2-
2
| ||
| 3 |
4
| ||
| 3 |
点评：本题主要考查了一次函数的综合题，解题的关键是要注意分段讨论函数关系式．
练习册系列答案
相关题目
如图，在直角△ABC中，CD是斜边AB上的高，∠BCD=35°，求：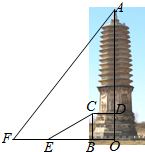
位于赤峰市宁城的“大明塔”是我国辽代的佛塔，距今已有1千多年的历史．如图，王强同学为测量大明塔的高度，在地面的点E处测得塔基BC上端C的仰角为30°，他又沿BE方向走了26米，到达点F处，测得塔顶端A的仰角为52°，已知塔基是以OB为半径的圆内接正八边形，B点在正八边形的一个顶点上，塔基半径OB=18米，塔基高BC=11米，求大明塔的高OA（结果保留到整数，
如图，已知BC是以AB为直径的⊙的切线，且BC=AB，连接OC交⊙O于点D，延长AD交BC于点E，F为BE上一点，且DF=FB．