题目内容
如图，在△ABC中，∠BAC=90°，BC的垂直平分线交BC于点E，交CA的延长线于D，交AB于点F，求证：AE2=EF•ED．
【考点】相似三角形的判定与性质．
【专题】证明题．
【分析】利用直角三角形的性质以及等角对等边得出∠B=∠EAB，∠B=∠D，进而得出△AEF∽△DEA，即可得出答案．
【解答】解：∵∠BAC=90°，
∴∠B+∠C=90°，∠D+∠C=90°，
∴∠B=∠D，
∵BC的垂直平分线交BC于点E，∠BAC=90°．
∴BE=EA，
∴∠B=∠BAE，
∴∠D=∠BAE，
∵∠FEA=∠AED，
∴△FEA∽△AED，
∴
=
∴AE2=EF•ED．
【点评】此题主要考查了相似三角形的判定与性质以及直角三角形的性质，根据已知得出∠EAB=∠D是解题关键．
练习册系列答案
备战中考寒假系列答案
相关题目
+
=2； 
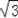
，连接AB，过AB中点C1分别作x轴和y轴的垂线，垂足分别是点A1、B1，连接A1B1，再过A1B1中点C2作x轴和y轴的垂线，照此规律依次作下去，则点Cn的坐标为 ．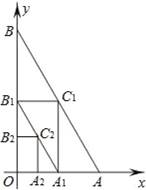
，则2xy的值为( )
D．