题目内容
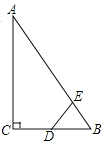
【题目】如图所示，山坡上有一棵与水平面垂直的大树，一场台风过后，大树被刮倾斜后折断倒在山坡上，树的顶部恰好接触到坡面．已知山坡的坡角∠AEF=23°，量得树干倾斜角∠BAC=38°，大树被折断部分和坡面所成的角∠ADC=60°，AD=4m．求这棵大树没有折断前的高度．(结果精确到个位，参考数据：
=1．4，
=1．7，
=2．4)．
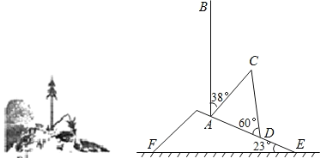
【答案】10米
【解析】
把
通过作高分割为两个有特殊角的直角三角形，所以先求
的大小，延长BA与EF相交，可得BA
EF，从而可求，过A作CD上的高后可得到答案．
解：如下图，延长BA交EF于N，过A作AFCD于F，
由题意得：BAEF，又因为：
，
所以
，
又因为
，
所以
．
因为AFCD，
，
所以
所以AF＝CF
因为AD＝4，
所以DF＝2，AF＝CF＝
，
所以AC＝
所以大树的高度为AC＋CD＝
10（米）
即大树没有折断前大约10米．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
