Question

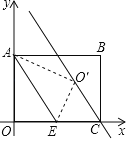
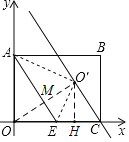
【题目】如图，在平面直角坐标系中，已知矩形OABC，点O为坐标原点，点A在y轴正半轴上，点C在x轴正半轴上，OA＝4，OC＝6，点E为OC的中点，将△OAE沿AE翻折，使点O落在点O′处，作直线CO'，则直线CO'的解析式为（　　）

A.y＝﹣x+6B.y＝﹣x+8C.y＝﹣x+10D.y＝﹣x+8

Answer 1

【答案】D

【解析】

连接OO'交AE与点M，过点O'作O'H⊥OC于点H，由轴对称的性质可知AE垂直平分OO'，先用面积法求出OM的长，进一步得出OO'的长，再证△AOE∽△OHO'，分别求出OH，O'H的长，得出点O'的坐标，再结合点C坐标即可用待定系数法求出直线CO'的解析式．

解：连接OO'交AE与点M，过点O'作O'H⊥OC于点H，

∴点E为OC中点，

∴OE＝EC＝OC＝3，

在Rt△AOE中，OE＝3，AO＝4，

∴AE＝＝5，

∵将△OAE沿AE翻折，使点O落在点O′处，

∴AE垂直平分OO'，

∴OM＝O'M，

在Rt△AOE中，

∵S△AOE＝AOOE＝AEOM，

∴×3×4＝×5×OM，

∴OM＝，

∴OO'＝，

∵∠O'OH+∠AOM＝90°，∠MAO+∠AOM＝90°，

∴∠MAO＝∠O'OH，

又∵∠AOE＝∠OHO'＝90°，

∴△AOE∽△OHO'，

∴＝＝，

即＝＝，

∴OH＝，O'H＝，

∴O'的坐标为（，），

将点O'（，），C（6，0）代入y＝kx+b，

得，，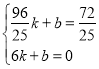

解得，k＝﹣，b＝8，

∴直线CO'的解析式为y＝﹣x+8，

故选：D．