题目内容
已知,在△ABC中,∠ACB=90°,CA=CB,D是直线AC上一点,连接BD,作AE⊥BD,垂足为E,连接EC.
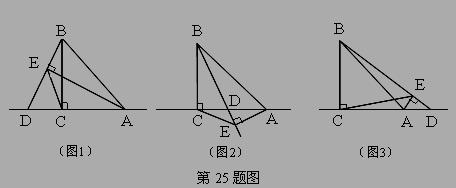
(1)如图1,D在AC延长线上,AC > CD,求证:EA-EB=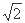 EC;
EC;
(2)当D在AC上(图2)或D在CA延长线上(图3)时,EA、EB、EC三条线段的数量关系如何?直接写出你探究的结论.
 |
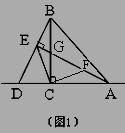
(1)证明:在AE上截取AF=EB,连接CF--------1
∵AE⊥BD
 ∴∠AEB=90°
∴∠AEB=90°
∴∠AEB=∠ACB=90°
又∵∠AGC=∠BGE
∴∠GAC=∠GBE------------------------------------------------2
又∵CA=CB,AF=BE
∴△FAC≌△EBC---------------------------------------------------------------------------3
∴FC=EC,∠ ACF=∠BCE
∴∠ECF=∠BCE+∠GCF=∠ ACF+∠GCF=∠ACB=90°----------------------------4
∴EF=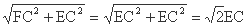 --------------------------------------5
--------------------------------------5
∴EA- EB= EA- AF= EF=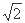 EC
EC
即EA- EB= 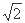 EC ---------------------------------------------------6
EC ---------------------------------------------------6
(2)当D在AC上(图2)时, EB- EA = 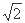 EC ---------
EC --------- ----------------9
----------------9
当 D在CA延长线上(图3)时,EA+EB= 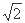 EC ----------------------12
EC ----------------------12

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
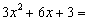 ;
;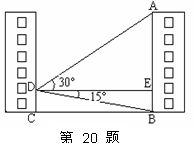 求楼AB的高度.
求楼AB的高度.

 A.
A.  B. C. D.
B. C. D.