题目内容
已知二次函数y=3（x-4）2的图象上有三点A（-1，y1）、B（
，y2）、C（5，y3），则y1、y2、y3的大小关系为 ．
| 2 |
考点：二次函数图象上点的坐标特征
专题：计算题
分析：先根据二次函数的性质得到抛物线的对称轴为直线x=4，然后比较三个点都直线x=4的远近得到y1、y2、y3的大小关系．
解答：解：∵二次函数的解析式为y=3（x-4）2，
∴抛物线的对称轴为直线x=4，
∵A（-1，y1）、B（
，y2）、C（5，y3），
∴点A离直线x=4最远，点C离直线x=4最近，
而抛物线开口向上，
∴y3＜y2＜y1．
故答案为y3＜y2＜y1．
∴抛物线的对称轴为直线x=4，
∵A（-1，y1）、B（
| 2 |
∴点A离直线x=4最远，点C离直线x=4最近，
而抛物线开口向上，
∴y3＜y2＜y1．
故答案为y3＜y2＜y1．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．
练习册系列答案
相关题目
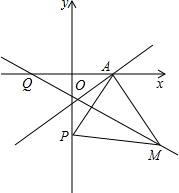如图，点A、B的坐标分别为（a，0）、（b，0）且
如图，AB⊥BD，CD⊥BD，AB=6cm，CD=4cm，BD=14cm，点p在BD上移动，当PB=
草原上有一个边长为5米的正方形木屋，A、B、C、D是木屋的角，在B点有一根木桩，用8米长的绳子把一匹马拴在木桩上，这匹马的活动范围是多少平方米？
如图，分别过点C、B作△ABC的BC边上的中线AD及延长线的垂线，垂足分别为E、F．求证：
如图，AB是圆O的半径，AC=7，AB=25，点D平分弧BC，则AD=