题目内容
已知抛物线y=| 1 | 2 |
(1)求c的取值范围;
(2)试确定直线y=cx+1经过的象限,并说明理由.
分析:(1)根据题意的判别式小于0,从而得出c的取值范围即可;
(2)根据c的值,判断直线所经过的象限即可.
(2)根据c的值,判断直线所经过的象限即可.
解答:解:(1)∵抛物线y=
x2+x+c与x轴没有交点.
∴△=1-4×
c=1-2c<0,
解得c>
;
(2)∵c>
,
∴直线过一、三象限,
∵b=1>0,
∴直线与y轴的交点在y轴的正半轴,
∴直线y=cx+1经过第一、二、三象限.
| 1 |
| 2 |
∴△=1-4×
| 1 |
| 2 |
解得c>
| 1 |
| 2 |
(2)∵c>
| 1 |
| 2 |
∴直线过一、三象限,
∵b=1>0,
∴直线与y轴的交点在y轴的正半轴,
∴直线y=cx+1经过第一、二、三象限.
点评:本题考查了抛物线和x轴的交点问题以及一次函数的性质,是基础知识要熟练掌握.

练习册系列答案
相关题目
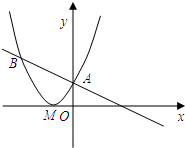 角形?若存在,求出点P的坐标;若不存在,请说明理由.
角形?若存在,求出点P的坐标;若不存在,请说明理由.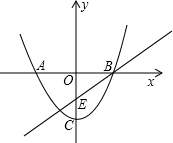 已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=
已知抛物线y=ax2+c与x轴交于A、B两点,与y轴交于C点,直线y=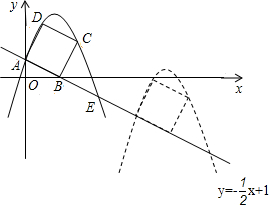
 如图,已知直线
如图,已知直线 +12x-19的顶点的横坐标是3,则a=________.
+12x-19的顶点的横坐标是3,则a=________.