题目内容
 如图,△ABC和△BDE都是等边三角形.请说明:
如图,△ABC和△BDE都是等边三角形.请说明:(1)AE=CD;
(2)△ABE≌△CBD.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)根据等边三角形各边长相等的性质,可得AB=BC,BE=BD,根据等边三角形各内角为60°可得∠ABE=∠DBE,进而求证△ABE≌△CBD(SAS),即可求得AE=CD;
(2)根据等边三角形的性质推出AB=BC,∠ABC=∠DBE=60°,BE=BD,根据SAS证出即可.
(2)根据等边三角形的性质推出AB=BC,∠ABC=∠DBE=60°,BE=BD,根据SAS证出即可.
解答:证明:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABE=60°
又∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠ABE=∠DBE,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS),
∴AE=CD.
(2)∵△ABC和△BDE都是等边三角形,
∴AB=BC,∠ABC=∠DBE=60°,BE=BD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD(SAS).
∴AB=BC,∠ABE=60°
又∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠ABE=∠DBE,
在△ABE和△CBD中,
|
∴△ABE≌△CBD(SAS),
∴AE=CD.
(2)∵△ABC和△BDE都是等边三角形,
∴AB=BC,∠ABC=∠DBE=60°,BE=BD,
在△ABE和△CBD中,
|
∴△ABE≌△CBD(SAS).
点评:本题主要考查对全等三角形的性质和判定,等边三角形的面积等知识点的理解和掌握,熟练地运用性质进行推理是解此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
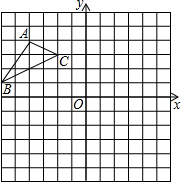 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,4)、B(-6,1)、C(-2,3),
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-4,4)、B(-6,1)、C(-2,3),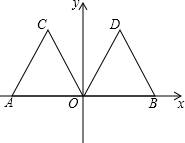 如图,在平面直角坐标系中,点A的坐标为(-4,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.
如图,在平面直角坐标系中,点A的坐标为(-4,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD.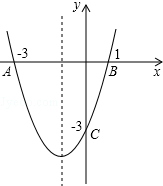 如图,抛物线l交x轴于点A(-3,0)、B(1,0),交y轴于点C(0,-3).将抛物线l沿y轴翻折得抛物线l1.
如图,抛物线l交x轴于点A(-3,0)、B(1,0),交y轴于点C(0,-3).将抛物线l沿y轴翻折得抛物线l1. 已知:如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.如果AC=2,CE=4.
已知:如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD.如果AC=2,CE=4. 如图,已知:b∥c,a⊥b.求证:a⊥c.
如图,已知:b∥c,a⊥b.求证:a⊥c.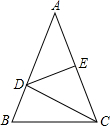 如图,△ABC中,AB=AC,D是AB边上的一点,DE垂直平分AC,∠A=40°,求∠BDC的度数.
如图,△ABC中,AB=AC,D是AB边上的一点,DE垂直平分AC,∠A=40°,求∠BDC的度数.