题目内容
20. 如图,△ABC中,∠C=90°.
如图,△ABC中,∠C=90°.(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=8,BC=6,求CP的长.
分析 (1)作∠BAC的平分线交BC于P点,则点P到点C的距离与点P到边AB的距离相等;
(2)作PD⊥AB于点,如图,根据角平分线性质得PD=PC,则可证明Rt△ADP≌Rt△ACP得到AD=AC=8,再利用勾股定理计算出AB=10,则BD=2,设PC=x,则PD=x,BP=6-x,在Rt△BDP中,利于勾股定理得(6-x)2=x2+22,然后解方程即可.
解答 解:(1)如图,点P即为所求;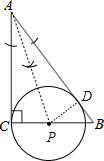
(2)作PD⊥AB于点,如图,
∵AP平分∠CAB,PD⊥AB于D,∠C=90°,
∴PD=PC.
在Rt△ADP和Rt△ACP中
$\left\{\begin{array}{l}{AP=AP}\\{PC=PD}\end{array}\right.$,
∴Rt△ADP≌Rt△ACP(HL),
∴AD=AC=8,
在Rt△ABC中,AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
∴BD=10-8=2,
设PC=x,则PD=x,BP=6-x,
在Rt△BDP中,∵PD2+BD2=PB2,
∴(6-x)2=x2+22,解得x=$\frac{8}{3}$.
答:CP的长为$\frac{8}{3}$.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了全等三角形的判定与性质和勾股定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15. 已知实数a在数轴上的位置如图所示,则化简|a+1|+|a|的结果为( )
已知实数a在数轴上的位置如图所示,则化简|a+1|+|a|的结果为( )
 已知实数a在数轴上的位置如图所示,则化简|a+1|+|a|的结果为( )
已知实数a在数轴上的位置如图所示,则化简|a+1|+|a|的结果为( )| A. | 1 | B. | 2 | C. | 2a+1 | D. | -2a-1 |
10.下列关系成立的是( )
| A. | a0=1 | B. | a3n÷an=a3 | C. | (-a)3÷(-a2)=a | D. | a+an-1=an |
 如图:∠A+∠B=90°,∠BCD+∠B=90°,可得∠A=∠BCD.理由是同角的余角相等.
如图:∠A+∠B=90°,∠BCD+∠B=90°,可得∠A=∠BCD.理由是同角的余角相等. 如图,已知数轴上有A、B、C三个点,它们表示的数分别是-24,-10,10.
如图,已知数轴上有A、B、C三个点,它们表示的数分别是-24,-10,10.