Question

3．如图，∠AOB=30°，点P是∠AOB内一点，PO=8，在∠AOB的两边上分别有点R、Q均不同于O）．
（1）求△PQR周长的最小值；
（2）当△PQR周长取最小值时，求∠QPR的值．

Answer 1

分析 （1）根据轴对称图形的性质，作出P关于OA、OB的对称点M、N，连接MN，根据两点之间线段最短得到最小值线段，根据等边三角形的性质解答即可；
（2）根据对称的性质求得∠OMN+∠ONM=∠OPQ+∠OPR，即可求得∠QPR的度数．

解答 解：（1）分别作P关于OA、OB的对称点M、N．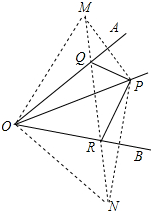
连接MN交OA、OB交于Q、R，则△PQR符合条件．
连接OM、ON，
由轴对称的性质可知，OM=ON=OP=8，
∠MON=∠MOP+∠NOP=2∠AOB=2×30°=60°，
则△MON为等边三角形，
∴MN=8，
∵QP=QM，RN=RP，
∴△PQR周长=MN=8，
（2）根据对称的性质得到∠OMN=∠OPQ，∠ONM=∠OPR，
∴∠OMN+∠ONM=∠OPQ+∠OPR，
∵△MON为等腰直角三角形，
∴∠OMN+∠ONM=120°，
∴∠OPQ+∠OPR=120°，
即∠QPR=120°

点评 本题考查了轴对称-最短路径问题，根据轴对称的性质作出对称点是解题的关键，掌握线段垂直平分线的性质和等边三角形的性质的灵活运用．