题目内容
5．
如图，在平行四边形ABCD中，过点C的直线CE⊥AB，垂足为E，若∠EAD=54°，则∠BCE的度数为（ ）| A． | 54° | B． | 36° | C． | 46° | D． | 126° |
分析 首先根据直角三角形两锐角互余可得∠2的度数，再根据平行四边形的性质可得AD∥BC，然后再根据两直线平行，同位角相等可得∠ECB=∠2=36°．
解答 
解：∵CE⊥AB，
∴∠E=90°，
∵∠EAD=54°，
∴∠2=90°-54°=36°，
∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠ECB=∠2=36°，
故选：B．
点评 此题主要考查了平行四边形的性质，关键是掌握平行四边形的两组对边分别平行．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．抛物线y=ax2+bx+c上部分点的横坐标x、纵坐标y的对应值如下表：
从上表可知，方程ax2+bx+c=4解是-1或2．
| x | … | -2 | -1 | 0 | 1 | … |
| y | … | 0 | 4 | 6 | 6 | … |
16．
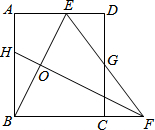如图，矩形ABCD中，AB=8，点E是AD上的一点，有AE=4，BE的垂直平分线交BC的延长线于点F，连结EF交CD于点G．若G是CD的中点，以下几个结论：
①∠AEB=∠BEF；②△BEF是等腰三角形；③△DEG与△BEF相似；④四边形ABCD的面积为56．
则以上正确的有（ ）
如图，矩形ABCD中，AB=8，点E是AD上的一点，有AE=4，BE的垂直平分线交BC的延长线于点F，连结EF交CD于点G．若G是CD的中点，以下几个结论：①∠AEB=∠BEF；②△BEF是等腰三角形；③△DEG与△BEF相似；④四边形ABCD的面积为56．
则以上正确的有（ ）
| A． | ①③ | B． | ②③④ | C． | ①② | D． | ①②④ |
13．下列计算正确的是（ ）
| A． | 5ab-3ab=2 | B． | （1+$\sqrt{2}$）（1-$\sqrt{2}$）=1 | C． | -（-a）4÷a2=a2 | D． | （xy）-2=$\frac{1}{{x}^{2}{y}^{2}}$ |
20．
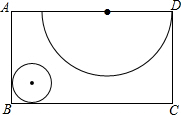如图，矩形ABCD纸板中，剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若已知小圆的半径为1cm，则此圆锥的全面积是（ ）
如图，矩形ABCD纸板中，剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若已知小圆的半径为1cm，则此圆锥的全面积是（ ）| A． | 2πcm | B． | 3πcm | C． | $\sqrt{3}$πcm | D． | （$\sqrt{3}$+1）πcm |
10．下列计算不正确的是（ ）
| A． | |-3|=3 | B． | （-$\frac{1}{4}$）2=$\frac{1}{16}$ | C． | -$\frac{5}{3}+\frac{1}{3}=-\frac{4}{3}$ | D． | $\sqrt{{{（{-2}）}^2}}$=-2 |
14．甲、乙两人每次都从五个数-2，-1，0，1，2中任取一个，分别记作（x，y），则这些坐标表示的点在直线y=x+1上的概率为（ ）
| A． | $\frac{4}{25}$ | B． | $\frac{8}{25}$ | C． | $\frac{9}{25}$ | D． | $\frac{2}{5}$ |
15．下列计算正确的是（ ）
| A． | -x2+3x2=2 | B． | x2×x3=x6 | ||
| C． | （x+1）（-x-1）=-x2-2x-1 | D． | $\frac{{x}^{2}-4}{x-2}$=x-2 |