题目内容
【题目】如图,将△ABC沿着射线BC方向平移至△A'B'C',使点A落在∠ACB的外角平分线CD上,连结AA′.
(1)判断四边形ACC′A的形状,并说明理由.
(2)在△ABC中,∠B=90°,AB=24,cos∠BAC=![]() ,求CB的长.
,求CB的长.
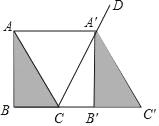
【答案】(1)四边形ACC'A'是菱形,理由详见解析;(2)CB=10.
【解析】
(1)根据平行四边形的判定定理(有一组对边平行且相等的四边形是平四边形)推知四边形ACC'A'是平行四边形.有一组邻边相等的平行四边形是菱形推知四边形ACC'A'是菱形.
(2)通过解直角△ABC得到AC的长,利用勾股定理即可得到BC的长度.
(1)四边形ACC'A'是菱形.理由如下:
由平移的性质得到:AC∥A′C′,且AC=A′C′,
则四边形ACC'A'是平行四边形.
又∵CD平分∠ACB的外角,
∴∠ACA′=∠A'CC',
∵AA'∥BB',
∴∠C'CA'=∠AA'C,
∴∠AA'C=∠ACA',
∴AA'=AC,
∴四边形ACC'A'是菱形.
(2)∵在△ABC中,∠B=90°,AB=24,cos∠BAC=![]() ,
,
∴cos∠BAC=![]() ,即
,即![]()
∴AC=26.
∴由勾股定理知: ![]()

练习册系列答案
相关题目