题目内容
【题目】己知一次函数
的图象与
轴、
轴分别交于
、
两点，将这条直线进行平移后交轴、轴分别交于
、
，要使点、、、构成的四边形面积为4，则直线
的解析式为__________．
【答案】
或
．
【解析】
先确定
、
点的坐标，利用两直线平移的问题设直线
的解析式为
，则可表示出
，
，
，讨论：当点
在
轴的正半轴时，利用三角形面积公式得到
，当点在轴的负半轴时，利用三角形面积公式得到
，然后分别解关于
的方程后确定满足条件的的直线解析式．
解：
一次函数
的图象与轴、
轴分别交于、两点，
，，
，
设直线的解析式为，
，，，
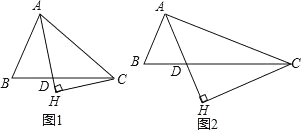
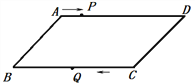
如图1，当点在轴的正半轴时，则
，
依题意得：，
解得
（舍去）或
，
此时直线的解析式为；
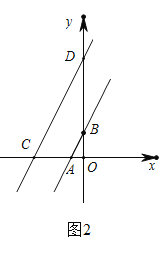
如图2，当点在轴的负半轴时，则
，
依题意得：，
解得
（舍去）或
，
此时直线的解析式为，
综上所述，直线的解析式为或．
故答案为：或．
练习册系列答案
名师点拨卷系列答案
相关题目
