Question

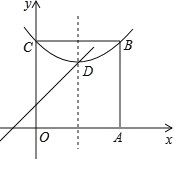
【题目】在如图的菱形网格图中，每个小菱形的边长均为个单位，且每个小菱形内角中的锐角为60°．

（1）直接写出的三个顶点的坐标；

（2）在图中作出以点为旋转中心，沿顺时针方向旋转60°后的图形；

（3）根据（2），请直接写出线段扫过的面积．

Answer 1

【答案】（1）A，B，C；（2）见解析；（3）．

【解析】

（1）分别过点A，B，C作x轴的垂线，垂足分别为D，E，F，分别过点A，C作y轴的垂线，垂足分别为G，H，根据菱形的性质以及矩形的判定与性质，分别求出各点的坐标即可；

（2）根据旋转的性质，由对应点与对应中心的连线分别相等且夹角为60°分别找出各个对应点，顺次连接即可；

（3）根据线段扫过的面积=扇形CPC1的面积-扇形APA1的面积求解即可．

解：（1）分别过点A，B，C作x轴的垂线，垂足分别为D，E，F，分别过点A，C作y轴的垂线，垂足分别为G，H，设GA的延长线与BE相交于点M，由题意得，

AG=1，AO=2，AB=3，BC=2，BH=3，∠AOD=∠BAM=60°，

由作图易知四边形OGAD为矩形，四边形MAED为矩形，四边形BEFC为矩形，

∴OD=AG=1，EF=BC=2，AM=DE，AD=ME．

在Rt△AOD中，AD=AO·sin∠AOD=2×sin60°=2×，∴点A的坐标为（1，）；

在Rt△ABM中，BM=AB·sin∠BAM=3×sin60°=3×，AM=AB=，

∴OE=OD+DE=0D+AM=1+=，BE=BM+ME=BM+AD=，∴点B的坐标为；

OF=OD+DE+EF=OD+AM+BC=1++2=，CF=BE=，∴点C的坐标为，

故点A，B，C三点的坐标分别为A，B，C．

（2）如图所示：

（3）根据题意可得，

线段扫过的面积=扇形CPC1的面积-扇形APA1的面积=．

故所求面积为．