题目内容
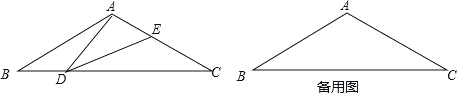
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
【答案】(1)证明见解析(2)y=![]() x+2(0<x<2
x+2(0<x<2![]() )(3)当△ADE是等腰三角形时,AE=4﹣2
)(3)当△ADE是等腰三角形时,AE=4﹣2![]() 或
或![]() .
.
【解析】
试题分析:(1)根据两角相等证明:△ABD∽△DCE;
(2)如图1,作高AF,根据直角三角形30°的性质求AF的长,根据勾股定理求BF的长,则可得BC的长,根据(1)中的相似列比例式可得函数关系式,并确定取值;
(3)分三种情况进行讨论:①当AD=DE时;②当AE=ED时;③当AD=AE时,讨论即可得到答案.
试题解析:(1)∵△ABC是等腰三角形,且∠BAC=120°,
∴∠ABD=∠ACB=30°,
∴∠ABD=∠ADE=30°,
∵∠ADC=∠ADE+∠EDC=∠ABD+∠DAB,
∴∠EDC=∠DAB,
∴△ABD∽△DCE;
(2)如图1,∵AB=AC=2,∠BAC=120°,
过A作AF⊥BC于F,
∴∠AFB=90°,
∵AB=2,∠ABF=30°,
∴AF=![]() AB=1,
AB=1,
∴BF=![]() ,
,
∴BC=2BF=2![]() ,
,
则DC=2![]() ﹣x,EC=2﹣y,
﹣x,EC=2﹣y,
∵△ABD∽△DCE,
∴![]() ,
,
∴![]() ,
,
化简得:y=![]() x+2(0<x<2
x+2(0<x<2![]() );
);
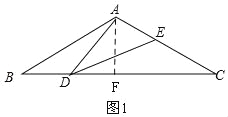
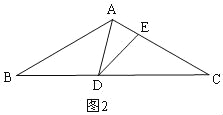
(3)当AD=DE时,如图2,
由(1)可知:此时△ABD∽△DCE,
则AB=CD,即2=2![]() ﹣x,
﹣x,
x=2![]() ﹣2,代入y=
﹣2,代入y=![]() x+2,
x+2,
解得:y=4﹣2![]() ,即AE=4﹣2
,即AE=4﹣2![]() ,
,
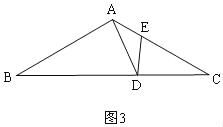
当AE=ED时,如图3,
∠EAD=∠EDA=30°,∠AED=120°,
∴∠DEC=60°,∠EDC=90°,
则ED=![]() EC,即y=
EC,即y=![]() (2﹣y),
(2﹣y),
解得:y=![]() ,即AE=
,即AE=![]() ,
,
当AD=AE时,
∠AED=∠EDA=30°,∠EAD=120°,
此时点D与点B重合,不符合题意,此情况不存在,
∴当△ADE是等腰三角形时,AE=4﹣2![]() 或
或![]() .
.

 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案