��Ŀ����
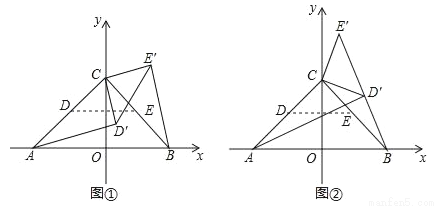
��ƽ��ֱ������ϵ�У��� A����2��0����B��2��0����C��0��2������ D����E�ֱ��� AC��BC���е㣬����CDE�Ƶ�C��ʱ����ת�õ���CD��E�䣬����ת��Ϊ�������� AD�䣬BE�䣮
��1����ͼ�٣��� 0�㣼����90�㣬�� AD���CE��ʱ������Ĵ�С��
��2����ͼ�ڣ��� 90�㣼����180�㣬���� D�������߶� BE����ʱ���� sin��CBE���ֵ��
��3����ֱ��AD����ֱ��BE���ཻ�ڵ�P�����P�ĺ�����m��ȡֵ��Χ��ֱ��д��������ɣ���
��ϰ��ϵ�д�
 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
�����Ŀ


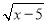 +
+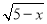 +2����x=_____��y=_____��
+2����x=_____��y=_____��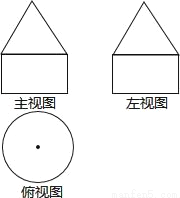
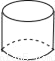 B.
B. 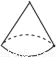 C.
C. 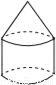 D.
D.