题目内容
为了创建全国卫生城,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送.若两车合作,各运12趟才能完成,需支付运费共4800元;若甲、乙两车单独运完此堆垃圾,则乙车所运趟数是甲车的2倍;已知乙车每趟运费比甲车少200元.
(1)分别 求出甲、乙两车每趟的运费;
求出甲、乙两车每趟的运费;
(2)若单独租用甲车运完此堆垃圾,需运多少趟;
 (3)若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中为x,y均为正整数.
(3)若同时租用甲、乙两车,则甲车运x趟,乙车运y趟,才能运完此堆垃圾,其中为x,y均为正整数.
① 当x =10时,y = ;
当y =10时,x = ;
② 求y与x的函数关系式.
探究:在(3)的条件下,设总运费为w(元).
①求w与x的函数关系式,直接写出w的最小值;
②当x≥10且y≥10时,甲车每趟的运费打7折,乙车每趟的运费打9折,直接写出w的最小值.
(1)解:设甲、乙两车每趟的运费分别为m元、n元,由题意得

解得: 
答:甲、乙两车每趟的运费分别为300元、100元 .
(2)解:设单独租用甲车运完此堆垃圾,需运a趟, 由题意得
12( )=1
)=1
解得 a=18
经检验a= 18是原方程的解
18是原方程的解
答:单独租用甲车运完此堆垃圾,需运18趟.
(3)① 16; 1 3 .
3 .
②解:
y=36-2x
探究:①w=300x+100y=300x+100(36-2x)
=100x+3600 (0<x<18,且x为正整数)
w的最小值3700元.
②解:
w=300×0.7x+100×0.9y=300×0.7x+100×0.9(36-2x)
=30x+3240
∵x≥10且y≥10
∴10≤x≤13,且x为正整数
w的最小值3540元.

实施新课改以来,某班学生经常采 用“小组合作学习”的方式进行学习.值周班长每周对各小组合作学习情况进行综合评分.下表是其中一周的评分结果:
用“小组合作学习”的方式进行学习.值周班长每周对各小组合作学习情况进行综合评分.下表是其中一周的评分结果:
| 组别 | 一 | 二 | 三 | 四 | 五 | 六 | 七 |
| 分值 | 90 | 96 | 89 | 90 | 91 | 85 | 90 |
“分值”这组数据的中位数和众数分别是( )
A.89,90 B.90,90 C.88,95 D.90,95

 D是线段AB上两点,已知图中所有线段的长度都是正整数,且总和为29,则线段AB的长度是
D是线段AB上两点,已知图中所有线段的长度都是正整数,且总和为29,则线段AB的长度是 
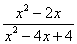 ÷
÷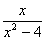 ,其中x的值是(1)中的正整数解.
,其中x的值是(1)中的正整数解. 的图象如图所示,则一次函数y=bx+
的图象如图所示,则一次函数y=bx+ 与反比例函数y=
与反比例函数y= 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )


 弃塑料袋对环境的影响,某班环保小组的六名同学记录了自己家中一周内丢弃的塑料袋的数量,结果如下(单位:个):33,25,28,26,25,31.如果该班有45位学生,那么根据提供的数据估计本周全班各家丢弃塑料袋的总数量约为 .
弃塑料袋对环境的影响,某班环保小组的六名同学记录了自己家中一周内丢弃的塑料袋的数量,结果如下(单位:个):33,25,28,26,25,31.如果该班有45位学生,那么根据提供的数据估计本周全班各家丢弃塑料袋的总数量约为 .