题目内容
(为方便答题,可在答题卡上画出你认为必要的图形)
在Rt△ABC中,∠A=90°,AC = AB = 4,D,E分别是边AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰RtRt△AD1E1,设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)如图1,当α=90°时,线段BD1的长等于 ,线段CE1的长等于 ;(直接填写结果)
(2)如图2,当α=135°时,求证:BD1 = CE1 ,且BD1 ⊥ CE1 ;
(3)求点P到AB所在直线的距离的最大值.(直接写出结果)
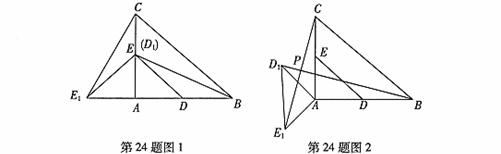
解:(1)BD1 = 2 ,CE1 = 2
,CE1 = 2 ……2分
……2分
(2)证明:当α=135°时,由旋转可知∠D1AB = E1AC = 135° ……3分
又AB=AC,AD1=AE1,∴△D1AB ≌ △E1AC ……4分
∴BD1=CE1 且 ∠D1BA = E1CA ……5分
设直线BD1与AC交于点F,有∠BFA=∠CFP ……6分
 ∴∠CPF=∠FAB=90°,∴BD1⊥CE1 ……7分
∴∠CPF=∠FAB=90°,∴BD1⊥CE1 ……7分
(3)1 +  ……11分
……11分
(四边形AD1PE1为正方形时,距离最大,此时PD1=2,PB=2+2 )
)

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 中 ,自变量x的取值范围是____________.
中 ,自变量x的取值范围是____________.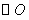 的直径,过点B作
的直径,过点B作 ,交AB于点F,且
,交AB于点F,且 ,链接AC,AD,延长AD交BM地点E。
,链接AC,AD,延长AD交BM地点E。 是等边三角形。
是等边三角形。 ,求OE的长。
,求OE的长。
 ,求代数式(a - 1)2 + b(2a + b)+ 2a 的值.
,求代数式(a - 1)2 + b(2a + b)+ 2a 的值.


