��Ŀ����
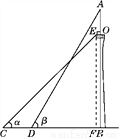
��ͼ��ij���۹��������ص�EΪ�ļ���Ŀ�������㣬��֪��E������������AB�ľ���OEΪ10�ף�����ABΪ123��(AB��ֱ����BC)���ڵ���C����õ�E�����Ǧ���45�㣬�ӵ�C��CB����ǰ��40����D�㣬��D���������A�����Ǧ£�60�㣬���E�����ĸ߶�EF.(�����ȷ��1�ף��ο�����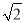 ��1.4��
��1.4�� 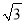 ��1.7)
��1.7)
��ϰ��ϵ�д�
�����Ŀ


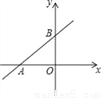
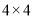 �������������У�ÿ��С�����εı߳�Ϊ1������
�������������У�ÿ��С�����εı߳�Ϊ1������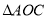 �Ƶ�O˳ʱ����ת90��õ�
�Ƶ�O˳ʱ����ת90��õ�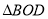 ����
����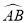 �ij��� ��
�ij��� ��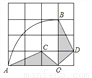
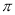 B. 6
B. 6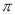 C. 3
C. 3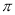 D. 1.5
D. 1.5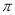
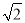 cos 45�㣭
cos 45�㣭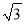 tan 60�㣻��2��tan230�㣫cos230�㣭sin245��tan 45��.
tan 60�㣻��2��tan230�㣫cos230�㣭sin245��tan 45��.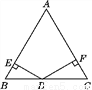
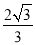 C.
C. 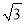 D.
D. 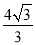
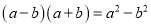
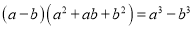
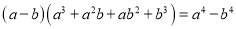
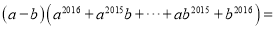 _______��
_______��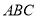 ��
�� 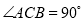 ��
�� 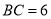 ����
����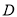 Ϊб��
Ϊб��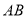 ���е㣬��
���е㣬��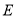 Ϊ��
Ϊ��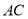 �ϵ�һ�����㣮����
�ϵ�һ�����㣮����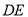 ������
������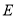 ��
��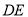 �Ĵ������
�Ĵ������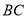 ���ڵ�
���ڵ�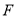 ����
����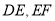 Ϊ�ڱ�������
Ϊ�ڱ�������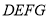 ��
��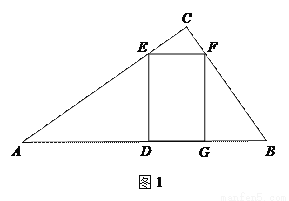
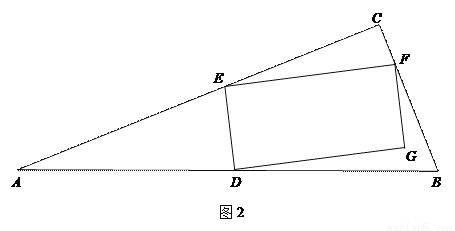
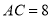 ����
����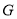 �ڱ�
�ڱ�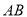 ��ʱ����DE��EF�ij���
��ʱ����DE��EF�ij���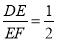 ����
����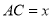 ������
������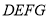 �����Ϊ
�����Ϊ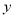 ����y����
����y����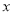 �ĺ�������ʽ��
�ĺ�������ʽ��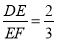 ���ҵ�
���ҵ�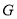 ǡ������Rt��
ǡ������Rt��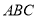 �ı��ϣ���
�ı��ϣ���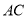 �ij���
�ij���