题目内容
7.在阳光下,小刚的影子长为2米,同时测得小刚的头顶距离其影子的顶端2.5米,若此时小刚旁边小树的影长为6米,则小树的高为4.5米.分析 根据题意可知小刚、地面和影子组成的三角形是直角三角形,先根据勾股定理求出小刚的身高,然后根据相似三角形对应边成比例求出小树的高即可.
解答 解:如图,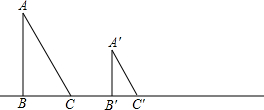
由题意得,A′C′=2.5米,B′C′=2米,
在Rt△A′B′C′中,A′B′=$\sqrt{2.{5}^{2}-{2}^{2}}$=1.5;
∵△ABC∽△A'B'C',
∴$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$,即$\frac{AB}{1.5}$=$\frac{6}{2}$,
解得:AB=4.5,
即小树高为4.5米.
故答案为4.5.
点评 此题考查了相似三角形在测量高度时的应用,解题的关键是找出题中的相似三角形,并建立适当的数学模型来解决问题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
15.下列事件中,不是必然事件的是( )
| A. | 对顶角相等 | B. | 九边形的外角和是360度 | ||
| C. | 内错角相等 | D. | 两点之间线段最短 |
2.网购越来越多地成为人们的一种消费方式,在刚刚过去的2015年11月11日的网上促销活动中,当天的全网交易额达到了惊人的1229亿元,其中1229亿元用科学记数法表示为( )
| A. | 1229×106 | B. | 1.229×1010 | C. | 122.9×108 | D. | 1.229×1011 |
16.一个两位数,它的十位数字比个位数字大3,且十位数字与个位数字的积是28,求这个两位数.设这个两位数的个位数字为x,则可列方程( )
| A. | x2+3x-28=0 | B. | x2-3x-28=0 | C. | x2+3x+28=0 | D. | x2-3x+28=0 |
17.如果从甲船看乙船,乙船在甲船的北偏东30°方向,那么从乙船看甲船,甲船在乙船的( )
| A. | 南偏西30°方向 | B. | 南偏西60°方向 | C. | 南偏东30°方向 | D. | 南偏东60°方向 |