题目内容
12.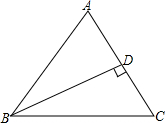 在△ABC中,∠ABC=45°,BD⊥AC于D,AD=3,DC=2,求△ABC的面积.
在△ABC中,∠ABC=45°,BD⊥AC于D,AD=3,DC=2,求△ABC的面积.
分析 把△ABD沿AB为对称轴翻折成为△ABG,△BCD沿BC为对称轴翻折成为△BCE,延长EB、GA相交于点F,根据轴对称的性质可以证明四边形BEFG是正方形,设BD=x,用x表示出AF、CF,在Rt△ACF中,根据勾股定理列式进行计算即可求出x的值,再利用三角形的面积公式列式计算即可得解.
解答 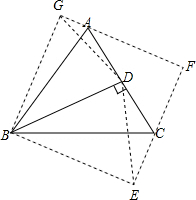 解:如图,把△BCD沿BC为对称轴翻折成为△BCE,△BDA沿AB为对称轴翻折成为△ABG,延长EC、GA相交于点F,
解:如图,把△BCD沿BC为对称轴翻折成为△BCE,△BDA沿AB为对称轴翻折成为△ABG,延长EC、GA相交于点F,
则△CBD≌△CBE,△BAD≌△BAG,
所以,BG=BD=BE,∠BEC=∠BGA=90°,
∵∠ABC=45°,
∴∠EBG=90°,
∴四边形BEFG是正方形,
∵AD=3,DC=2,
∴AC=AD+CD=3+2=5,
设BD=x,则CF=EF-CE=x-2,AF=FG-AG=x-3,
在Rt△ACF中,根据勾股定理,AF2+CF2=AC2,
即(x-3)2+(x-2)2=52,
整理得,x2-5x-6=0,
解得x1=-1(舍去),x2=6,
所以S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×5×6=15.
点评 本题考查了正方形的判定与性质,轴对称的性质,以及勾股定理的应用,根据∠ABC=45°轴对称图形,构造出正方形并得到Rt△ACF是解题的关键,也是本题的难点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
1.下列说法中,正确的个数为( )
①有公共顶点,没有公共边的两个角是对顶角
②相等的两个角是对顶角
③如果两个角是对顶角,那么这两个角相等
④如果一个角的两边分别是另一个角两边的反向延长线,这两个角是对顶角
⑤如果两个角不相等,那么这两个角不是对顶角.
①有公共顶点,没有公共边的两个角是对顶角
②相等的两个角是对顶角
③如果两个角是对顶角,那么这两个角相等
④如果一个角的两边分别是另一个角两边的反向延长线,这两个角是对顶角
⑤如果两个角不相等,那么这两个角不是对顶角.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.衣柜不透明的盒子中有3个红球和2个白球,它们除颜色外都相同,若从中任何摸出一个球,则下列叙述正确的是( )
| A. | 摸到红球是必然事件 | B. | 摸到黑球与摸到白球是随机事件 | ||
| C. | 摸到红球比摸到白球的可能性大 | D. | 摸到白球比摸到红球的可能性大 |
 已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC=6$\sqrt{2}$.
已知:如图,AB是⊙O的直径,AB=6,延长AB到点C,使BC=AB,D是⊙O上一点,DC=6$\sqrt{2}$.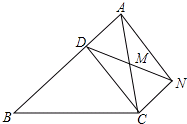 已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.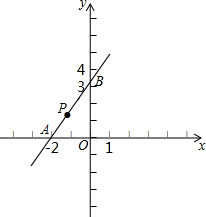 如图,直线y=$\sqrt{3}$x+2$\sqrt{3}$与x轴交于点A,与y轴交于点B,动点P从点A开始沿折线AB-BO以1cm/s的速度运动到点O.设点P运动的时间为t(s),△PAO面积为S(cm2).(坐标轴的单位长度为cm)
如图,直线y=$\sqrt{3}$x+2$\sqrt{3}$与x轴交于点A,与y轴交于点B,动点P从点A开始沿折线AB-BO以1cm/s的速度运动到点O.设点P运动的时间为t(s),△PAO面积为S(cm2).(坐标轴的单位长度为cm)