题目内容
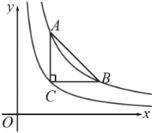
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 轴,点
轴,点![]() 、
、![]() 都在反比例函数
都在反比例函数![]() 上,点
上,点![]() 在反比例函数
在反比例函数![]() 上,则
上,则![]() ______.
______.
【答案】![]()
【解析】
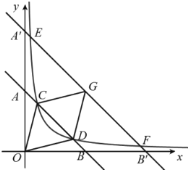
根据反比例函数的性质及等腰直角三角形的性质知:它们都是轴对称图形,且对称轴是直线![]() ,判断出点
,判断出点![]() 在直线
在直线![]() 上,证得四边形OECD为正方形,四边形OGBD、EGBC为矩形,再根据反比例函数k的几何意义,求得正方形和矩形的面积继而求得边长,得到答案.
上,证得四边形OECD为正方形,四边形OGBD、EGBC为矩形,再根据反比例函数k的几何意义,求得正方形和矩形的面积继而求得边长,得到答案.
因为反比例函数的图象是轴对称图形,所以反比例函数![]() 和
和![]() 的图象的对称轴都是直线
的图象的对称轴都是直线![]() .
.
∵在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
又![]() 轴,点
轴,点![]() 、
、![]() 都在反比例函数
都在反比例函数![]() 上,
上,
∴点![]() 在直线
在直线![]() 上.
上.
延长AC、BC分别交 x轴、y轴于点E、D,过点B作BG⊥x轴于G,
∵ ![]() 轴,
轴,![]() ,点
,点![]() 在直线
在直线![]() 上,
上,
∴四边形OECD为正方形,四边形OGBD、EGBC为矩形,
∵点![]() 在反比例函数
在反比例函数![]() 上,
上,
∴![]() ,
,
∴![]()
∴![]() ,
,
∵点![]() 在反比例函数
在反比例函数![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在等腰![]() 中,
中,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]()


练习册系列答案
相关题目