题目内容
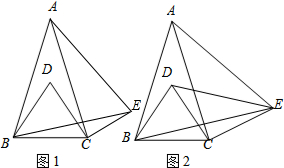
8.在△ABC中,AB=AC,∠BAC=α(0°<α<60°),分别以AB、BC为边作等边三角形ABE和等边三角形BCD,连结CE,如图1所示.(1)直接写出∠ABD的大小(用含α的式子表示);
(2)判断DC与CE的位置关系,并加以证明;
(3)在(2)的条件下,连结DE,如图2,若∠DEC=45°,求α的值.
分析 (1)根据等腰三角形的性质得到∠ABC=∠ACB=$\frac{1}{2}({180°-∠α})$=90°-$\frac{1}{2}$∠α,根据角的和差即可得到结论;
(2)连接AD;根据已知条件得到∠ABD=∠EBC,推出△ABD≌△EBC,根据全等三角形的性质得到∠ADB=∠ECB,证得△ABD≌△ACD,由全等三角形的性质得到∠BAD=∠CAD=$\frac{1}{2}$∠α,根据三角形的内角和得到∠BDA=180°-∠ABD-∠BAD=180°-(30°-$\frac{1}{2}$∠α )-$\frac{1}{2}$∠α=150°,求得∠BCE=150°,即可得到结论.
(3)根据已知条件得到△DEC为等腰三角形,根据等腰直角三角形的性质得到DC=DE=BC,根据三角形的内角和得到∠EBC=15°,即可得到结论.
解答 解:(1)∵AB=AC,∠A=∠α,
∴∠ABC=∠ACB=$\frac{1}{2}({180°-∠α})$
=90°-$\frac{1}{2}$∠α
∴∠ABD=∠ABC-∠ABE
=90°-$\frac{1}{2}$∠α-60°
=30°-$\frac{1}{2}$∠α;
(2)DC与CE垂直;
连接AD;
∵∠ABE=∠DBC=60°,
∴∠ABE-∠DBE=∠DBC-∠DBE,
即∠ABD=∠EBC,
在△ABD和△EBC中,
$\left\{\begin{array}{l}AB=BE\\∠ABD=∠EBC\\ BD=BC\end{array}\right.$,
∴△ABD≌△EBC,
∴∠ADB=∠ECB,
在△ABD和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{AD=AD}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ACD,
∴∠BAD=∠CAD=$\frac{1}{2}$∠α,
∴∠BDA=180°-∠ABD-∠BAD=180°-(30°-$\frac{1}{2}$∠α )-$\frac{1}{2}$∠α=150°,
∴∠BCE=150°,
∵∠BCD=60°,
∴∠DCE=90°,
即DC与CE垂直;
(3)∵∠DCE=90°,
又∵∠DEC=45°,
∴△DEC为等腰三角形,
∴DC=CE=BC,
∵∠BCE=150°,
∴∠EBC=15°,
∵∠EBC=30°-$\frac{1}{2}$∠α=15°,
∴∠α=30°.
点评 本题考查了全等三角形的性质,等腰三角形的判定和性质,三角形的内角和,熟练掌握全等三角形的性质是解题的关键.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | -2 | B. | 0 | C. | 2 | D. | 3 |
| A. | 1 | B. | -1 | C. | -$\frac{1}{2}$ | D. | 0 |
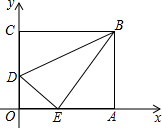 如图所示,把矩形OABC放入平面直角坐标系中,点B坐标为(10,8),点D是OC上一动点,将矩形OABC沿直线BD折叠,点C恰好落在OA上的点E处,则点D的坐标是( )
如图所示,把矩形OABC放入平面直角坐标系中,点B坐标为(10,8),点D是OC上一动点,将矩形OABC沿直线BD折叠,点C恰好落在OA上的点E处,则点D的坐标是( )| A. | (0,4) | B. | (0,5) | C. | (0,3) | D. | (3,0) |
 如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为( )
如图,该表面展开图按虚线折叠成正方体后,相对面上的两个数互为相反数,则(x+y)的值为( )| A. | -2 | B. | -3 | C. | 2 | D. | 1 |
 一只小狗在如图所示的地板上走来走去,地板是由大小相等的小正方形铺成的.求最终停在黑色方砖上的可能性是多少.
一只小狗在如图所示的地板上走来走去,地板是由大小相等的小正方形铺成的.求最终停在黑色方砖上的可能性是多少.