题目内容
4.先化简,再求值:($\frac{{a}^{2}-1}{{a}^{2}-2a+1}$-$\frac{1}{1-a}$)÷$\frac{2}{{a}^{2}-1}$,其中a是方程x2+3x+1=0的根.分析 将分子、分母因式分解,约分后再将括号内的部分通分,然后将除法转化为乘法,进行化简;然后将a2+3a=-1整体代入即可.
解答 解:原式=[$\frac{(a-1)(a+1)}{(a-1)^{2}}$+$\frac{1}{a-1}$]×$\frac{(a-1)(a+1)}{2}$
=($\frac{a+1}{a-1}$+$\frac{1}{a-1}$)×$\frac{(a-1)(a+1)}{2}$
=$\frac{a+2}{a-1}$×$\frac{(a-1)(a+1)}{2}$
=$\frac{{a}^{2}+3a+3}{2}$,
∵a是方程x2+3x+1=0的根,
∴a2+3a+1=0,
∴a2+3a=-1,
∴原式=$\frac{-1+3}{2}$=1.
点评 本题考查了分式的化简求值、一元二次方程的解,熟悉因式分解是解题的关键.

练习册系列答案
相关题目
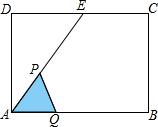 如图,在矩形ABCD中,AB=4cm,AD=2$\sqrt{3}$cm,E为CD边上的中点,点P从点A沿AE运动到点E,点Q从点A沿AB运动到点B时,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系式是y=$\frac{\sqrt{3}}{4}$t2(0<t≤4).
如图,在矩形ABCD中,AB=4cm,AD=2$\sqrt{3}$cm,E为CD边上的中点,点P从点A沿AE运动到点E,点Q从点A沿AB运动到点B时,它们运动的速度都是1cm/s.如果点P,Q同时开始运动,设运动时间为t(s),△APQ的面积为y(cm2),则y与t的函数关系式是y=$\frac{\sqrt{3}}{4}$t2(0<t≤4). 如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)
如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O-C-B-A-O的路线移动(即:沿着长方形移动一周)