题目内容
有四张形状、大小和质地相同的卡片A、B、C、D,正面分别写有一个正多边形(所有正多边形的边长相等),把四张卡片洗匀后正面朝下放在桌面上,从中随机抽取一张(不放回),接着再随机抽取一张.

(1)请你用画树形图或列表的方法列举出可能出现的所有结果;
(2)如果在(1)中各种结果被选中的可能性相同,求两次抽取的正多边形能构成平面镶嵌的概率;
(3)若两种正多边形构成平面镶嵌,p、q表示这两种正多边形的个数,x、y表示对应正多边形的每个内角的度数,则有方程px+qy=360,求每种平面镶嵌中p、q的值.
见解析
【解析】
试题分析:(1)根据所画树形图或列表可知所有出现的结果共有12种;(2)所有出现的12种结果中两次抽取的正多边形能构成平面镶嵌有4种,所以概率是 ;(3)若两种正多边形构成平面镶嵌,只能是正三角形和正方形及正三角形和六边形,所以x、y的值是60,90和60,120,分别代入px+qy=360,求整数解即可.
;(3)若两种正多边形构成平面镶嵌,只能是正三角形和正方形及正三角形和六边形,所以x、y的值是60,90和60,120,分别代入px+qy=360,求整数解即可.
试题解析:(1)所有出现的结果共有如下12种:
第一次/第二次 | A | B | C | D |
A | BA | CA | DA | |
B | AB | CB | DB | |
C | AC | BC | DC | |
D | AD | BD | CD |
(2)因为12种结果中能构成平面镶嵌的有4种:AB,BA,AD,DA
所以P(两次抽取的正多边形能构成平面镶嵌)= =
= ;
;
(3)当正三角形和正方形构成平面镶嵌时,
则有60p+90q=360,即2p+3q=12.
因为p、q是正整数,
所以p=3,q=2,
当正三角形和六边形构成平面镶嵌时,
则有60p+120q=360,即p+2q=6.
因为p、q是正整数,
所以p=4,q=1或p=2,q=2.
考点:1. 画树形图或列表求概率;2. 平面镶嵌;3.二元一次方程的整数解.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 B.﹣1 C.0 D.1
B.﹣1 C.0 D.1 <n+1,则n的值为( )
<n+1,则n的值为( ) ,1中,最大的实数是( )
,1中,最大的实数是( ) 的图象先沿
的图象先沿 轴向上平移3个单位,再沿
轴向上平移3个单位,再沿 轴向右平移2个单位后得到的图象对应的函数关系式为 .
轴向右平移2个单位后得到的图象对应的函数关系式为 . (
( <0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,
<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0, ),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则
),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则 的值是( )
的值是( )
 B.
B. C.
C. D.
D.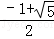

 B.
B. C.
C. D.
D.