题目内容
如图,反比例函数 (
( <0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,
<0)的图象经过点A(﹣1,1),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0, ),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则
),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B′在此反比例函数的图象上,则 的值是( )
的值是( )

A. B.
B. C.
C. D.
D.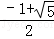
A
【解析】
试题分析:把点A(﹣1,1)代入 得k=-1,所以
得k=-1,所以 ,做出点B关于直线l称轴点B′,连结B B′,PB′,根据题意可得AB=OB=1,所以∠AOB=∠BAO=45°,又直线l垂直于OA,所以△B PB′是等腰直角三角形,且∠B PB′=90°,所以PB′=PB=t-1,所以点B′的坐标是(t-1,t),代入
,做出点B关于直线l称轴点B′,连结B B′,PB′,根据题意可得AB=OB=1,所以∠AOB=∠BAO=45°,又直线l垂直于OA,所以△B PB′是等腰直角三角形,且∠B PB′=90°,所以PB′=PB=t-1,所以点B′的坐标是(t-1,t),代入 整理得
整理得 解得
解得 ,因为t>0,所以t=
,因为t>0,所以t= ,故选:A.
,故选:A.
考点:1. 反比例函数;2.等腰直角三角形的判定与性质;3.一元二次方程.

练习册系列答案
相关题目

 最接近的是( )
最接近的是( )

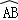 的长等于( )
的长等于( ) B.
B. C.
C. D.
D.

 CD.
CD. B.
B. C.
C. D.
D.