题目内容
 如图,在等腰三角形ABC中,AB=AC,以A为圆心的⊙A与边BC相切于点D.与AB、AC两边分别交于点E、F.连接DE、DF、EF.
如图,在等腰三角形ABC中,AB=AC,以A为圆心的⊙A与边BC相切于点D.与AB、AC两边分别交于点E、F.连接DE、DF、EF.(1)求证:DE=DF;
(2)若0A的半径为3,BC=8.求EF的长.
考点:切线的性质,全等三角形的判定与性质,相似三角形的判定与性质
专题:
分析:(1)通过全等三角形的判定定理SAS证得△AED≌△AFD,则该全等三角形的对应边相等;
(2)根据等腰△AEF、等腰△ABC“三合一”的性质证得AD⊥EF,AD⊥BC,则EF∥BC,所以△AEF∽△ABC,然后根据相似三角形的对应边成比例来求线段EF的长度.
(2)根据等腰△AEF、等腰△ABC“三合一”的性质证得AD⊥EF,AD⊥BC,则EF∥BC,所以△AEF∽△ABC,然后根据相似三角形的对应边成比例来求线段EF的长度.
解答: (1)证明:如图,连接AD.
(1)证明:如图,连接AD.
∵⊙A与边BC相切于点D,
∴AD⊥BC.
又∵AB=AC,
∴∠EAD=∠FAD.
∵在△AED与△AFD中,
,
∴△AED≌△AFD(SAS),
∴DE=DF;
(2)解:∵AB=AC,AD⊥BC,
∴BD=DC=4.
又∵0A的半径为3,即AD=3,
∴根据勾股定理求得AC=
=5;
∵AE=AF,∠EAD=∠FAD,
∴AD⊥EF.
又∵AD⊥BC,
∴EF∥BC,
∴△AEF∽△ABC,
∴
=
,即
=
,
∴EF=
.
 (1)证明:如图,连接AD.
(1)证明:如图,连接AD.∵⊙A与边BC相切于点D,
∴AD⊥BC.
又∵AB=AC,
∴∠EAD=∠FAD.
∵在△AED与△AFD中,
|
∴△AED≌△AFD(SAS),
∴DE=DF;
(2)解:∵AB=AC,AD⊥BC,
∴BD=DC=4.
又∵0A的半径为3,即AD=3,
∴根据勾股定理求得AC=
| AD2+DC2 |
∵AE=AF,∠EAD=∠FAD,
∴AD⊥EF.
又∵AD⊥BC,
∴EF∥BC,
∴△AEF∽△ABC,
∴
| EF |
| BC |
| AF |
| AC |
| EF |
| 8 |
| 3 |
| 5 |
∴EF=
| 24 |
| 5 |
点评:本题综合考查了相似三角形的判定与性质、全等三角形的判定与性质以及切线的性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
观察下列图形,第1个图形中有4个三角形,第二个图形中有12个三角形,…,则第10个图形中三角形的个数是( )


| A、4000 | B、92 |
| C、76 | D、84 |
若x=-2是关于x的方程2x+3m+1=0的解,则m的值为( )
A、
| ||
B、-
| ||
| C、-1 | ||
| D、1 |
下列分式变形错误的是( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
 已知集合A中的数与集合B中对应的数之间的关系是某个二次函数.若用x表示集合A中的数,用y表示集合B中的数,由于粗心,小颖算错了集合B中的一个y值,请你指出这个算错的y值为
已知集合A中的数与集合B中对应的数之间的关系是某个二次函数.若用x表示集合A中的数,用y表示集合B中的数,由于粗心,小颖算错了集合B中的一个y值,请你指出这个算错的y值为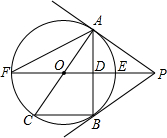 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D.交⊙O于点A,延长AD与⊙0交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D.交⊙O于点A,延长AD与⊙0交于点C,连接BC,AF. 如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,OA=5,AB=2.点E在线段OC上,作∠MEN=∠AOC,使∠MEN的一边始终经过点A,另一边交线段BC于点F,连接AF.
如图,一条抛物线经过原点和点C(8,0),A、B是该抛物线上的两点,AB∥x轴,OA=5,AB=2.点E在线段OC上,作∠MEN=∠AOC,使∠MEN的一边始终经过点A,另一边交线段BC于点F,连接AF.