题目内容
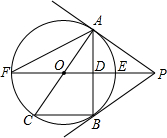 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D.交⊙O于点A,延长AD与⊙0交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E、F,过点B作PO的垂线BA,垂足为点D.交⊙O于点A,延长AD与⊙0交于点C,连接BC,AF.(1)求证:直线PA为⊙O的切线;
(2)若tan∠F=
| 1 |
| 2 |
考点:切线的判定与性质,全等三角形的判定与性质,解直角三角形
专题:
分析:(1)连接OB,证明△POB≌△POA,根据全等三角形的对应角相等证得∠OAP=90°,即直线PA为⊙O的切线;
(2)连接AE,构建直角△AEF.在该直角三角形中利用锐角三角函数的定义、勾股定理可设AE=x,AF=2x,进而可得EF=
x;然后由面积法求得AD=
x,所以根据垂径定理求得AB的长度,在Rt△ABC中,根据勾股定理易求BC=
x;最后由余弦三角函数的定义求解.
(2)连接AE,构建直角△AEF.在该直角三角形中利用锐角三角函数的定义、勾股定理可设AE=x,AF=2x,进而可得EF=
| 5 |
2
| ||
| 5 |
3
| ||
| 5 |
解答: 解:(l)证明:连接OB,
解:(l)证明:连接OB,
∵PB与圆O相切,
∴PB⊥OB,即∠OBP=90°,
∵OP⊥AB,
∴D为AB中点,即OP垂直平分AB,
∴PA=PB,
∵在△OAP和△OBP中,
,
∴△OAP≌△OBP(SSS),
∴∠OAP=∠OBP=90°,
∴AP⊥OA,
则直线PA为⊙O的切线;
(2)连接AE,则∠FAE=90°.
∵tan∠F=
,
∴
=
,
∴可设AE=x,AF=2x,
则由勾股定理,得
EF=
=
x,
∵
AE•AF=
EF•AD,
∴AD=
x.
又∵AB⊥EF,
∴AB=2AD=
x,
∴Rt△ABC中,AC=
x,AB=
x,
∴BC=
x
∴cos∠ACB=
=
.
 解:(l)证明:连接OB,
解:(l)证明:连接OB,∵PB与圆O相切,
∴PB⊥OB,即∠OBP=90°,
∵OP⊥AB,
∴D为AB中点,即OP垂直平分AB,
∴PA=PB,
∵在△OAP和△OBP中,
|
∴△OAP≌△OBP(SSS),
∴∠OAP=∠OBP=90°,
∴AP⊥OA,
则直线PA为⊙O的切线;
(2)连接AE,则∠FAE=90°.
∵tan∠F=
| 1 |
| 2 |
∴
| AE |
| AF |
| 1 |
| 2 |
∴可设AE=x,AF=2x,
则由勾股定理,得
EF=
| AF2+AE2 |
| 5 |
∵
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=
2
| ||
| 5 |
又∵AB⊥EF,
∴AB=2AD=
4
| ||
| 5 |
∴Rt△ABC中,AC=
| 5 |
4
| ||
| 5 |
∴BC=
3
| ||
| 5 |
∴cos∠ACB=
| BC |
| AC |
| 3 |
| 5 |
点评:此题考查了切线的判定与性质,全等三角形的判定与性质,熟练掌握切线的判定与性质是解本题的关键.

练习册系列答案
相关题目
下列调查方式合适的是( )
| A、为了了解九年级学生数学作业的时间,校长对九年级一班的3位同学进行了抽样调查 |
| B、为了了解全国青少年的睡眠时间,调研人员对某市七年级学生进行了调查 |
| C、为了了解重庆人民对建设“五个重庆”的感受,记者到某中学随机采访了20名老师 |
| D、为了了解我国新引进的一架飞机的安全性能,检查人员采用了普查的方式 |
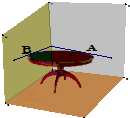 小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )
小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )| A、45° |
| B、135° |
| C、45°或135° |
| D、90°或135° |
 某批发商6月1日以70元/千克的成本价购入了某海产品1 000千克,据市场预测,该产品的销售价y(元/千克)与时间x(天)之间函数关系的图象如图中的折线段ABC所示.
某批发商6月1日以70元/千克的成本价购入了某海产品1 000千克,据市场预测,该产品的销售价y(元/千克)与时间x(天)之间函数关系的图象如图中的折线段ABC所示. 如图,在等腰三角形ABC中,AB=AC,以A为圆心的⊙A与边BC相切于点D.与AB、AC两边分别交于点E、F.连接DE、DF、EF.
如图,在等腰三角形ABC中,AB=AC,以A为圆心的⊙A与边BC相切于点D.与AB、AC两边分别交于点E、F.连接DE、DF、EF.