题目内容
18. 如图.在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,BE=CF,AB∥ED.求证:∠F=∠ACB.
如图.在△ABC和△DEF中,B、E、C、F在同一直线上,AB=DE,BE=CF,AB∥ED.求证:∠F=∠ACB.
分析 由BE=CF可得BC=EF,由AB∥DE可得∠B=∠DEF,可证明△ABC≌△DEF,可得∠F=∠ACB.
解答 证明:
∵BE=CF,
∴BE+EC=EC+CF,
即BC=EF,
∵AB∥DE,
∴∠B=∠DEF,
在△ABC和△DEF中
$\left\{\begin{array}{l}{AB=DE}\\{∠B=∠DEF}\\{BC=EF}\end{array}\right.$
∴△ABC≌△DEF(SAS),
∴∠F=∠ACB.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(即全等三角形的对应边相等、对应角相等)是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.甲、乙两个同学分别解一道一元二次方程,甲因把一次项系数看错了,而解得方程两根为-3和5,乙把常数项看错了,解得两根为2和2,则原方程是( )
| A. | x2+4x-15=0 | B. | x2-4x-15=0 | C. | x2+4x+15=0 | D. | x2-4x-15=0 |

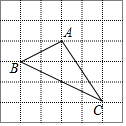 如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.