题目内容
如图，梯形ABCD的两底BC=2AD，O为其内部一点，使得△AOD的面积与△BOE的面积之和是4，E是OC的中点．则梯形ABCD的面积是
- A.8
- B.12
- C.16
- D.20
B
分析：欲求梯形的面积，先求上下底边和高，可设O点到AD的垂直距离为h1，O点到BC的垂直距离为h2，表示出△AOD的面积和△BOE的面积，再代入梯形的面积公式，即可求解．
解答：设O点到AD的垂直距离为h1，则△AOD的面积=
•AD•h1，
设O点到BC的垂直距离为h2，则△BOC的面积=•BC•h2，
∵E是OC的中点，
∴△BOE的面积：三角形BOC的面积=1：2，
S△BOE=••BC•h2，
∴•AD•h1+••BC•h2=4，
又BC=2AD，代入上式可得：AD•（h1+h2）=4，
设为梯形的高为h，可得：AD•h=8，
梯形ABCD面积=•（AD+BC）•h=（AD+2AD）•h=×3×AD•h=×3×8=12．
故选B．
点评：本题考查了梯形的面积问题，难度较大，关键求出AD与h的积，间接的求出梯形的面积．
分析：欲求梯形的面积，先求上下底边和高，可设O点到AD的垂直距离为h1，O点到BC的垂直距离为h2，表示出△AOD的面积和△BOE的面积，再代入梯形的面积公式，即可求解．
解答：设O点到AD的垂直距离为h1，则△AOD的面积=
•AD•h1，设O点到BC的垂直距离为h2，则△BOC的面积=
•BC•h2，∵E是OC的中点，
∴△BOE的面积：三角形BOC的面积=1：2，
S△BOE=
••BC•h2，∴
•AD•h1+••BC•h2=4，又BC=2AD，代入上式可得：
AD•（h1+h2）=4，设为梯形的高为h，可得：AD•h=8，
梯形ABCD面积=
•（AD+BC）•h=（AD+2AD）•h=×3×AD•h=×3×8=12．故选B．
点评：本题考查了梯形的面积问题，难度较大，关键求出AD与h的积，间接的求出梯形的面积．
练习册系列答案
相关题目
如图，梯形ABCD的对角线交于点O，有以下四个结论：①△AOB∽△COD，②△AOD∽△ACB，③S△DOC：S△AOD=DC：AB，④S△AOD=S△BOC，其中始终正确的有（ ）个．
| A、1 | B、2 | C、3 | D、4 |
14、如图，梯形ABCD的两条对角线交于点E，图中面积相等的三角形共有
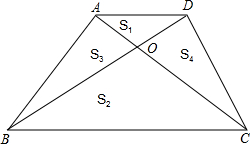如图，梯形ABCD的对角线AC、BD相交于点O，△ADO的面积记作S1，△BCO的面积记作S2，△ABO的面积记作S3，△CDO的面积记作S4，则下列关系正确是（ ）| A、S1=S2 | B、S1×S2=S3×S4 | C、S1+S2=S4+S3 | D、S2=2S3 |
16、如图，梯形ABCD的对角线交于点O，有以下三个结论：
如图，梯形ABCD的面积为34cm2，AE=BF，CE与DF相交于O，△OCD的面积为11cm2，则阴影部分的面积为