题目内容
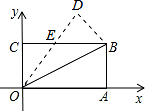
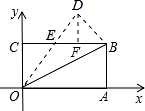
如图,在矩形 OABC 中,OA=8,OC=4,沿对角线 OB 折叠后,点 A 与点 D 重合,OD 与 BC
交于点 E,则点 D 的坐标是( )
A.(4,8) B.(5,8) C.(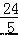 ,
,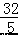 ) D.(
) D.(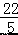 ,
,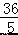 )
)
C【考点】翻折变换(折叠问题);坐标与图形性质.
【专题】计算题;压轴题.
【分析】由四边形 ABCD 为矩形,利用矩形的性质得到两对边相等,再利用折叠的性质得到 OA=OD, 两对角相等,利用 HL 得到直角三角形 BOC 与直角三角形 BOD 全等,利用全等三角形对应角相等 及等角对等边得到 OE=EB,在直角三角形 OCE 中,设 CE=x,表示出 OE,利用勾股定理求出 x 的 值,确定出 CE 与 OE 的长,进而由三角形 COE 与三角形 DEF 相似,求出 DF 与 EF 的长,即可确 定出 D 坐标.
【解答】解:∵矩形 ABCO 中,OA=8,OC=4,
∴BC=OA=8,AB=OC=4,
由折叠得到 OD=OA=BC,∠AOB=∠DOB,∠ODB=∠BAO=90°, 在 Rt△CBO 和 Rt△DOB 中,
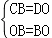 ,
,
∴Rt△CBO≌Rt△DOB(HL),
∴∠CBO=∠DOB,
∴OE=EB,
设 CE=x,则 EB=OE=8﹣x,
在 Rt△COE 中,根据勾股定理得:(8﹣x)2=x2+42, 解得:x=3,
∴CE=3,OE=5,DE=3,
过 D 作 DF⊥BC,可得△COE∽△FDE,
∴ 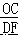 =
= 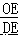 =
= 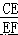 ,即
,即 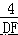 =
= 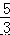 =
= 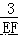 , 解得:DF=
, 解得:DF= 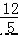 ,EF=
,EF= 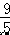 ,
,
∴DF+OC= 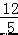 +4=
+4= 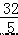 ,CF=3+
,CF=3+ 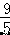 =
= 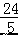 ,
,
则 D(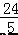 ,
,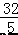 ), 故选 C.
), 故选 C.
【点评】此题考查了翻折变换(折叠问题),坐标与图形性质,全等三角形的判定与性质,勾股定理, 熟练掌握折叠的性质是解本题的关键.

 B.
B. 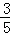 C.
C. 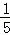 D.
D. 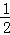
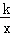 与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=
与直线y2=﹣x﹣(k+1)在第二象限的交点.AB⊥x轴于B,且S△ABO=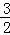 .
.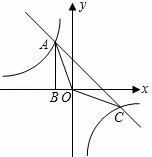 (1)求这两个函数的解析式;
(1)求这两个函数的解析式;