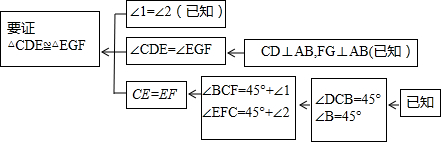
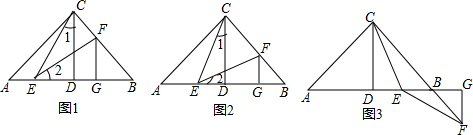
题目内容
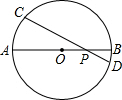 ⊙O的直径AB和弦CD相交于点P,已知AP=9cm,PB=3cm,∠CPA=30°,求弦CD的长.
⊙O的直径AB和弦CD相交于点P,已知AP=9cm,PB=3cm,∠CPA=30°,求弦CD的长.考点:垂径定理,含30度角的直角三角形,勾股定理
专题:
分析:过点O作OE⊥CD于点E,连接OC,先根据AP=9cm,PB=3cm得出AB=12cm,故可得出OP=3cm,再由直角三角形的性质求出OE的长,根据勾股定理求出CE的长,由垂径定理即可得出结论.
解答:
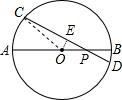 解:过点O作OE⊥CD于点E,连接OC,
解:过点O作OE⊥CD于点E,连接OC,
∵AP=9cm,PB=3cm,
∴AB=12cm,
∴OC=OB=6cm,
∴OP=6-3=3cm.
∵∠CPA=30°,
∴OE=
OP=
(cm),
∴CE=
=
(cm).
∵OE过点O且OE⊥CD,
∴CD=2CE=3
(cm).
 解:过点O作OE⊥CD于点E,连接OC,
解:过点O作OE⊥CD于点E,连接OC,∵AP=9cm,PB=3cm,
∴AB=12cm,
∴OC=OB=6cm,
∴OP=6-3=3cm.
∵∠CPA=30°,
∴OE=
| 1 |
| 2 |
| 3 |
| 2 |
∴CE=
62-(
|
3
| ||
| 2 |
∵OE过点O且OE⊥CD,
∴CD=2CE=3
| 15 |
点评:本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
下列各数中是无理数的是( )
| A、-1 | ||
| B、3.141 | ||
C、
| ||
D、
|
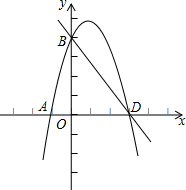 如图,在平面直角坐标系中,己知二次函数y=ax2+
如图,在平面直角坐标系中,己知二次函数y=ax2+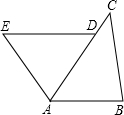 如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE,线段BC和AE相等吗?为什么?
如图,已知D是AC上一点,AB=DA,DE∥AB,∠B=∠DAE,线段BC和AE相等吗?为什么?