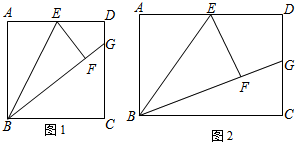
题目内容
(1)如图1,正方形ABCD的边长为1,点E是AD边的中点,将△ABE沿BE翻折得到△FBE,延长BF交CD边于点G,则FG=DG,求出此时DG的值;
(2)如图2,矩形ABCD中,AD>AB,AB=1,点E是AD边的中点,同样将△ABE沿BE翻折得到△FBE,延长BF交CD边于点G.
①证明:FG=DG;
②若点G恰是CD边的中点,求AD的值;
③若△ABE与△BCG相似,求AD的值.
(1)解:设DG为x,
由题意得:BG=1+x,CG=1-x,
由勾股定理得:BG2=BC2+CG2,
有:(1+x)2=12+(1-x)2,
解得: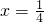 .
.
∴DG= ;
;
(2)①证明:连接EG,
∵△FBE是由△ABE翻折得到的,
∴AE=FE,∠EFB=∠EAB=90°,
∴∠EFG=∠EDG=90°.
∵AE=DE,
∴FE=DE.
∵EG=EG,
∴Rt△EFG≌Rt△EDG(HL).
∴DG=FG;
②解:若G是CD的中点,则DG=CG= ,
,
在Rt△BCG中,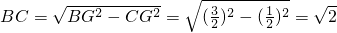 ,
,
∴AD= .
.
③解:由题意AB∥CD,
∴∠ABG=∠CGB.
∵△FBE是由△ABE翻折得到的,
∴∠ABE=∠FBE= ∠ABG,
∠ABG,
∴∠ABE= ∠CGB.
∠CGB.
∴若△ABE与△BCG相似,则必有∠ABE=∠CBG=30°.
在Rt△ABE中,AE=ABtan∠ABE= ,
,
∴AD=2AE= .
.
分析:(1)首先设DG为x,则由正方形的性质即可求得BG与CG的值,利用勾股定理构造方程,解方程即可求得DG的值;
(2)①首先连接EG,由△FBE是由△ABE翻折得到的,利用HL,即可求得Rt△EFG≌Rt△EDG,则可证得DG=FG;
②由G是CD的中点,得到DG与CG的值,在Rt△BCG中,利用勾股定理即可求得AD的长;
③由平行线与翻折变换的性质,易得:∠ABE= ∠CGB,又由相似三角形的性质与三角函数的性质,即可求得AD的值.
∠CGB,又由相似三角形的性质与三角函数的性质,即可求得AD的值.
点评:此题考查了翻折变换的性质,相似三角形的性质,全等三角形的判定与性质以及勾股定理等知识.此题综合性很强,注意数形结合与方程思想的应用.
由题意得:BG=1+x,CG=1-x,
由勾股定理得:BG2=BC2+CG2,
有:(1+x)2=12+(1-x)2,
解得:
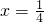 .
.∴DG=
 ;
;(2)①证明:连接EG,
∵△FBE是由△ABE翻折得到的,
∴AE=FE,∠EFB=∠EAB=90°,
∴∠EFG=∠EDG=90°.
∵AE=DE,
∴FE=DE.
∵EG=EG,
∴Rt△EFG≌Rt△EDG(HL).
∴DG=FG;
②解:若G是CD的中点,则DG=CG=
 ,
,在Rt△BCG中,
 ,
,∴AD=
 .
.③解:由题意AB∥CD,
∴∠ABG=∠CGB.
∵△FBE是由△ABE翻折得到的,
∴∠ABE=∠FBE=
 ∠ABG,
∠ABG,∴∠ABE=
 ∠CGB.
∠CGB.∴若△ABE与△BCG相似,则必有∠ABE=∠CBG=30°.
在Rt△ABE中,AE=ABtan∠ABE=
 ,
,∴AD=2AE=
 .
.分析:(1)首先设DG为x,则由正方形的性质即可求得BG与CG的值,利用勾股定理构造方程,解方程即可求得DG的值;
(2)①首先连接EG,由△FBE是由△ABE翻折得到的,利用HL,即可求得Rt△EFG≌Rt△EDG,则可证得DG=FG;
②由G是CD的中点,得到DG与CG的值,在Rt△BCG中,利用勾股定理即可求得AD的长;
③由平行线与翻折变换的性质,易得:∠ABE=
 ∠CGB,又由相似三角形的性质与三角函数的性质,即可求得AD的值.
∠CGB,又由相似三角形的性质与三角函数的性质,即可求得AD的值.点评:此题考查了翻折变换的性质,相似三角形的性质,全等三角形的判定与性质以及勾股定理等知识.此题综合性很强,注意数形结合与方程思想的应用.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
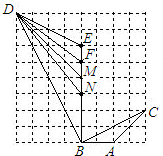 如图,在正方形网格上,与△ABC相似的三角形是( )
如图,在正方形网格上,与△ABC相似的三角形是( )| A、△NBD | B、△MBD | C、△EBD | D、△FBD |
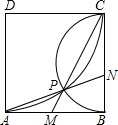 如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于( )
如图,在正方形ABCD内,以D点为圆心,AD长为半径的弧与以BC为直径的半圆交于点P,延长CP、AP交AB、BC于点M、N.若AB=2,则AP等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
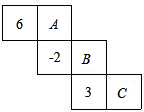 如图,是正方形的表面展形图,如果相对两个面数字之和相等,且A+B+C=14,则6A-2B+3C=
如图,是正方形的表面展形图,如果相对两个面数字之和相等,且A+B+C=14,则6A-2B+3C=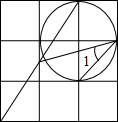 如图,在正方形网格图中,每个小正方形的边长均为 1,则∠1的正弦值是
如图,在正方形网格图中,每个小正方形的边长均为 1,则∠1的正弦值是 如图,在正方形ABCD中,E是BC上一点,且BC:EC=4:1,F是DC的中点.
如图,在正方形ABCD中,E是BC上一点,且BC:EC=4:1,F是DC的中点.