题目内容
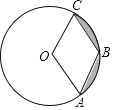
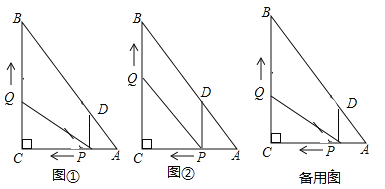
【题目】将一大、一小两个等腰直角三角形拼在一起,![]() ,连接
,连接![]() .
.
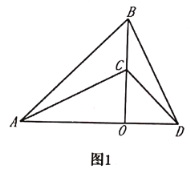
(1)如图1,若![]() 三点在同一条直线上,则
三点在同一条直线上,则![]() 与
与![]() 的关系是 ;
的关系是 ;
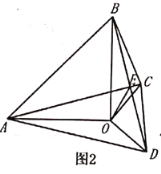
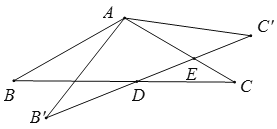
(2)如图2,若![]() 三点不在同一条直线上,
三点不在同一条直线上,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,猜想
,猜想![]() 之间的数量关系,并给予证明;
之间的数量关系,并给予证明;
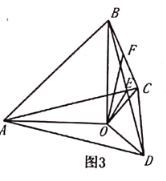
(3)如图3,在(2)的条件下作![]() 的中点
的中点![]() ,连接
,连接![]() ,直接写出
,直接写出![]() 与
与![]() 之间的关系.
之间的关系.
【答案】(1)![]() 且
且![]() ;(2)
;(2)![]() ;证明见解析;(3)
;证明见解析;(3)![]() 且
且![]() .
.
【解析】
(1)根据题意利用全等三角形的判定与性质以及延长AC交BD于点C’进行角的等量代换进行分析即可;
(2)根据题意在![]() 上截取
上截取![]() ,连接
,连接![]() ,并全等三角形的判定证明
,并全等三角形的判定证明![]() 和
和![]() ,进而利用勾股定理得出
,进而利用勾股定理得出![]() 进行分析求解即可;
进行分析求解即可;
(3)过点B作BM∥OC,交OF的延长线于点M,延长FO交AD于点N,证明BFMCFO,AODOBM,进而即可得到结论.
解:![]() ∵
∵![]() ,
,
∴![]() ,
,
延长AC交BD于点C’,如下图:
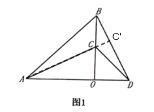
∵![]()
![]() ,
,
∴![]() ,
,
即![]() ,综上
,综上![]() 且
且![]() ,
,
故答案为:![]() 且
且![]() ;
;
![]()
证明:在![]() 上截取
上截取![]() ,连接
,连接![]()

![]()
![]()
![]()
在![]() 和
和![]() 中
中
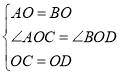
![]()
![]()
在![]() 和
和![]() 中
中
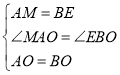
![]()
![]()
![]()
![]()
![]()
即![]()
![]()
![]()
![]() ;
;
![]() 且
且![]() ,理由如下:
,理由如下:
过点B作BM∥OC,交OF的延长线于点M,延长FO交AD于点N,
∵BM∥OC,
∴∠M=∠FOC,
∵∠BFM=∠CFO,BF=CF,
∴BFMCFO(AAS),
∴OF=MF,BM=CO,
∵DO=CO,
∴DO=BM,
∵BM∥OC,
∴∠OBM+∠BOC=180°,
∵∠BOC+∠AOD=360°-90°-90°=180°,
∴∠OBM=∠AOD,
又∵AO=BO,
∴AODOBM(SAS),
∴AD=OM=2OF ,∠BOM=∠OAD,
∵∠BOM+∠AON=180°-90°=90°,
∴∠OAD+∠AON=90°,即OF⊥AD.
∴![]() 且
且![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目