Question

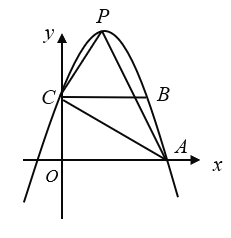
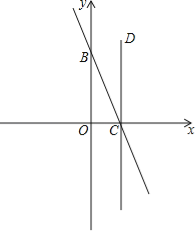
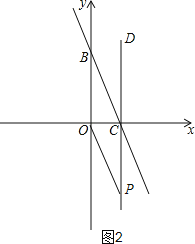
【题目】如图，直线y=-2x+4与坐标轴分别交于C、B两点，过点C作CD⊥x轴，点P是x轴下方直线CD上的一点，且△OCP与△OBC相似，求过点P的双曲线解析式．

Answer 1

【答案】或．

【解析】

由直线y=-2x+4与坐标轴分别交于C、B两点，易得OC=2，OB=4，再分两种情况①当∠OBC=∠COP时，△OCP与△OBC相似，②当∠OBC=∠CPO时，△OCP与△OBC相似分别求出点的坐标，再求出过点P的双曲线解析式即可．

∵直线y=-2x+4与坐标轴分别交于C、B两点，

∴令y=0，可得-2x+4=0，解得x=2，即C（2，0），OC=2，

令x=0，可得y=4，即B（0，4），OB=4，

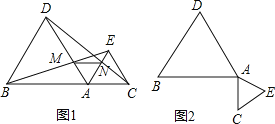
①如图1，当∠OBC=∠COP时，△OCP与△OBC相似，

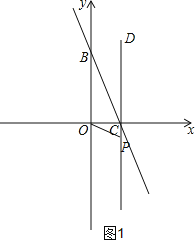
∴，即，解得CP=1，

∴P（2，-1），

设过点P的双曲线解析式y=，把P点代入得-1=，解得k=-2，

∴过点P的双曲线解析式，

②如图2，当∠OBC=∠CPO时，△OCP与△OBC相似，

在△OCP和△COB中，

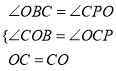
∴△OCP≌△COB（AAS）

∴CP=BO=4，

∴P（2，-4）

设过点P的双曲线解析式y=，把P点代入得-4=，解得k=-8，

∴过点P的双曲线解析式．

综上所述，过点P的双曲线解析式为：或．